Задача: Моторний човен пройшов 8 км за течією річки і 5 км проти течії, затративши на весь шлях 1 год. Знайти швидкість човна у стоячій воді, якщо швидкість течії річки дорівнює 3 км/год.
Рішення: Нехай х км/год — швидкість човна в стоячій воді, тоді швидкість човна за течією — х+3 км/год, а проти течії — х-3 км/год. Човен пройшов 8 км за течією 8/(х+3) год, а проти течії — 5/(х-3) год. Весь шлях човен пройшов за 1 год. Складемо і вирішимо рівняння.
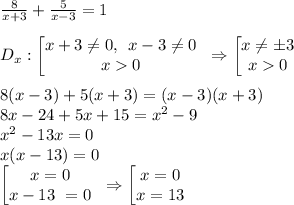
Відповідь: Швидкість човна у стоячій воді дорівню 13 км/год.
Область определения функции будет [2;+бесконечности) потому что у нас под корнем должно стоять не отрицательное число.
Решаем уравнение. Т.к. в правой части никогда не будет отрицательного числа(область определения не позволит) мы может возвести обе части уравнения в квадрат и получим
25(х-2)=х²+4х+4
Оно сводится к обычному квадратному
Х²+4х+4-25х+50=0
Х²-21х+54=0
По т. Виетта проиведение равняется колфиценту С, а сумма с противоположным знаком колфиценту В
Х1+Х2=21
Х1*Х2=54
Подходят числа 3 и 18, которые оба входят в область определения, значит оба являются ответом (можете решить через дискриминант, если вам удобно, тоже самое получите)
ответ:1)область определения [2;+бесконечности)
2) Х1=3 Х2=18
=2√m+2√n
б) (m⅓ + 3n½)² + (m⅓ - 3n½)²=
=m^2/3+6m^1/3n^1/2+9n+m^2/3-6m^1/3n^1/2+9n=2∛m²+18n
в) (m½ - 2n¼) (m½ + 2n¼)=m-4√n
г) (m½ - 3n) (m + 3m½n + 9n²)=m^3/2-27n³=√m³-27n³