Чтобы оценить периметр исходного треугольника, нужно сложить заданные неравенства
2,3 ≤ a ≤ 2,4
3,2 ≤ в ≤ 3,3
4,5 ≤ c ≤ 4,6
2,3+3,2+4,5 ≤ a+в+с ≤ 2,4+3,3+4,6
10 ≤ P ≤ 10,3
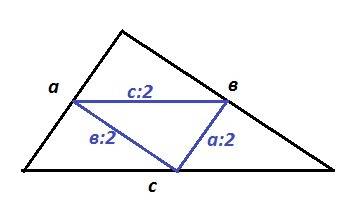
Соединили середины сторон, то есть провели 3 средние линии треугольника. Каждая средняя линия равна половине стороны, которой параллельна. Значит, периметр образованного треугольника равен половине периметра исходного треугольника
10 ≤ P ≤ 10,3 | : 2
10:2 ≤ P:2 ≤ 10,3 :2
5 ≤ P₁ ≤ 5,15
ответ : периметр полученного треугольника в пределах от 5 см до 5,15 см включительно.
√(12-x²-x)/√(x+3).
Подкоренное значение в числителе не может быть меньше нуля, поэтому 12-x²-x≥0, или все равно, что х²+х-12≤0, решается методом интервалов. сначала по теореме, обратной теореме Виета, угадываем корни левой части это - 4 и 3, потом раскладываем левую часть на множители, (х-3)(х+4)≤0, дальше разбиваем числовую ось на интервалы и определяем знак на каждом из них, выбирая для проверки любое число из этого интервала. например, для (-4;3) берем нуль. подставляем в неравенство (0-3)(0+4) минус на плюс дает минус. Знак на остальных интервалах так же определяется. результат ниже на рис.
-43 рис.
+ - +
Решением будет [-4;3]; со знаменателем проще. Там надо решить неравенство линейное, а именно х+3>0; x>-3 неравенство строгое, т.к. делить на нуль нельзя. Ведь мы про знаменатель..
Теперь пересекаем эти два решения, т.е. выбираем общее и получаем ответ. (-3;3]
(4x²-2x-1)(2x+1)=8x³+4x²-4x²-2x-2x-1
8x³-8x-16x²+16=8x³-4x-1
8x³-8x-16x²+16-8x³+4x+1=0
-4x+16x²+17=0
16x²-4x+17=0