1 кран заполняет 1 бассейн за х часов, а второй кран за у=(х-3) часа.
Производительность 1 крана равна 1/х бассейна в час, а производительность 2 крана равна 1/(х-3) бассейна в час.
Совместная производительность двух кранов равна 1/х+1/(х-3) бассейна в час.
Вместе оба крана заполняют бассейн за 6 ч 40 мин=6 и 2/3 часа=20/3 часа.
Формула работы: A=p*t , где р - производительность, t - время. Объём работы принимаем за 1.
Тогда совместная производительность обоих кранов равна 1/(20/3)=3/20 бассейна в час .
Составим уравнение:
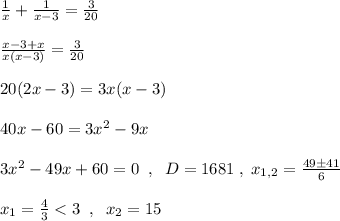
Число, меньшее 3, не подходит, т.к. по условию x>3.
Бассейн заполняется 1 краном за 15 часов, а 2 краном за 15-3=12 часов.
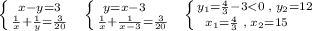
= (sin²x)² + (cos²x)² +2sin²x*cos²x -2sin²x*cos²x =
= (sin²x + cos²x)² -2sin²x*cos²x = 1² - 2*(sinx*cosx)² = 1-2*9/64 =
= 1 - 9/32 = 23/32
Если sin x-cos x = 1/2, то
(sin x-cos x)² = 1/4
sin²x + cos²x - 2sinx*cosx = 1/4
1 - 2sinx*cosx = 1/4 (основное тригонометрическое тождество)
2sinx*cosx = 3/4
sinx*cosx = 3/8
(sinx*cosx)² = 9/64