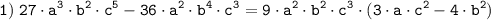
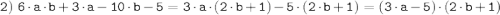
В решении.
Объяснение:
Первое задание.
Координаты точек пересечения графиком осей координат:
(-2; 0) и (0; -4)
Уравнение функции у = kx + b
Подставить в это уравнение первые известные значения х= -2 и у=0.
Получим первое уравнение системы:
k * (-2) + b = 0;
Подставить в это же уравнение вторые значения х= 0 и у= -4.
Получим второе уравнение системы:
k * 0 + b = -4
Решить систему:
k * (-2) + b = 0;
k * 0 + b = -4
Из второго уравнения b = -4, подставить в первое и вычислить k:
-2k - 4 = 0
-2k = 4
k = 4/-2
k = -2.
Подставить вычисленные значения k и b в уравнение у=kx + b и получить нужное уравнение:
у = -2х - 4.
Второе задание.
Координаты точек пересечения графиком осей координат:
(-4; 0) и (0; 2)
Уравнение функции у = kx + b
Подставить в это уравнение первые известные значения х= -4 и у=0.
Получим первое уравнение системы:
k * (-4) + b = 0;
Подставить в это же уравнение вторые значения х= 0 и у= 2.
Получим второе уравнение системы:
k * 0 + b = 2
Решить систему:
k * (-4) + b = 0;
k * 0 + b = 2
Из второго уравнения b = 2, подставить в первое и вычислить k:
-4k + 2 = 0
-4k = -2
k = -2/-4
k = 0,5.
Подставить вычисленные значения k и b в уравнение у=kx + b и получить нужное уравнение:
у = 0,5х + 2.
Миниатюрная и довольно простая задача из разряда тех, которые служат кругом плавающему студенту. На природе сонное царство середины июля, поэтому самое время устроиться с ноутбуком на пляже. Ранним утром заиграл солнечный зайчик теории, чтобы в скором времени сфокусироваться на практике, которая, несмотря на заявленную лёгкость, содержит осколки стекла в песке. В этой связи рекомендую добросовестно рассмотреть немногочисленные примеры этой странички. Для решения практических заданий необходимо уметь находить производные и понимать материал статьи Интервалы монотонности и экстремумы функции.
Сначала коротко о главном. На уроке о непрерывности функции я приводил определение непрерывности в точке и непрерывности на интервале. Образцово-показательное поведение функции на отрезке формулируется похожим образом. Функция непрерывна на отрезке если:
1) она непрерывна на интервале ;
2) непрерывна в точке справа и в точке слева.
Во втором пункте речь зашла о так называемой односторонней непрерывности функции в точке. Существует несколько подходов к её определению, но я буду придерживаться начатой ранее линии:
Функция непрерывна в точке справа, если она определена в данной точке и её правосторонний предел совпадает со значением функции в данной точке: . Она же непрерывна в точке слева, если определена в данной точке и её левосторонний предел равен значению в этой точке:
Представьте, что зелёные точки – это гвозди, на которых закреплена волшебная резинка:
Наибольшее и наименьшее значения функции на отрезке
Мысленно возьмите красную линию в руки. Очевидно, что как бы далеко мы не растягивали график вверх и вниз (вдоль оси ), функция всё равно останется ограниченной – изгородь сверху, изгородь снизу, и наше изделие пасётся в загоне. Таким образом, непрерывная на отрезке функция ограничена на нём. В курсе матанализа этот вроде бы простой факт констатируется и строго доказывается первой теоремой Вейерштрасса. …Многих раздражает, что в математике нудно обосновываются элементарные утверждения, однако в этом есть важный смысл. Предположим, некий житель махрового средневековья вытягивал график в небо за пределы видимости вот это вставляло. До изобретения телескопа ограниченность функции в космосе была вовсе не очевидна! Действительно, откуда вы знаете, что нас ждёт за горизонтом? Ведь когда-то и Земля считалась плоской, поэтому сегодня даже обыденная телепортация требует доказательства =)
Согласно второй теореме Вейерштрасса, непрерывная на отрезке функция достигает своей точной верхней грани и своей точной нижней грани .
Число также называют максимальным значением функции на отрезке и обозначают через , а число – минимальным значением функции на отрезке с пометкой .
В нашем случае:
Примечание: в теории распространены записи .
Грубо говоря, наибольшее значение находится там, где самая высокая точка графика, а наименьшее – где самая низкая точка.
Важно! Как уже заострялось внимание в статье об экстремумах функции, наибольшее значение функции и наименьшее значение функции – НЕ ТО ЖЕ САМОЕ, что максимум функции и минимум функции. Так, в рассматриваемом примере число является минимумом функции, но не минимальным значением.
Кстати, а что происходит вне отрезка ? Да хоть потоп, в контексте рассматриваемой задачи это нас совершенно не интересует. Задание предполагает лишь нахождение двух чисел и всё «Всё