Question

Найти область определения функции
50 !

a)

б)

в)

​

Answer 1

Объяснение:

а)

Знаменатель > 0, поэтому для нахождения области определения решим неравенство

$\sqrt{2-x}\geq 0; 2-x\geq 0; -x\geq -2; x\leq 2$

x∈(-∞;2]

б)

Знаменатель не должен быть равен 0, поэтому для нахождения области определения решим неравенство

$x^2-2x+30$

Дискриминант = 4-12 = -8<0, корней нет, a=1>0, ветви вверх,

значит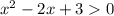 $x^2-2x+30$ при всех x∈(-∞;+∞) - это и есть область определения

в)

Знаменатель не должен быть равен 0, в нашем случае x^2+4 > 0 при всех x∈(-∞;+∞) - это и есть область определения