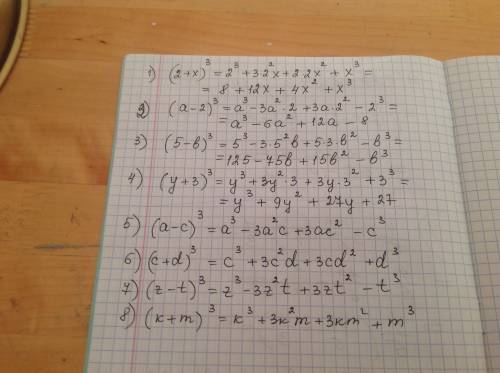
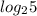 и
и 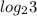
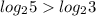
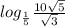 и
и 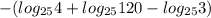
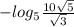 и
и 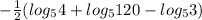
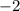 и надо бы не забыть поменять в этом месте знак неравенства.
и надо бы не забыть поменять в этом месте знак неравенства.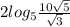 и
и 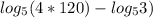
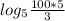 и
и 
 и
и 
 и
и 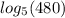
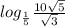 <
< 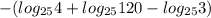
1) уравнение стороны АВ.
Найдем уравнение АВ, проходящей через две заданные точки A и В
\begin{gathered}\displaystyle \dfrac{x-x_1}{x_2-x_1}= \dfrac{y-y_1}{y_2-y_1} \\ \\ \\ \frac{x+2}{1+2}= \frac{y+3}{6+3} \\ \\ \boxed{y-3x-3=0} \end{gathered}x2−x1x−x1=y2−y1y−y11+2x+2=6+3y+3y−3x−3=0
2) Уравнение высоты CH
\dfrac{x-x_0}{A}= \dfrac{y-y_0}{B}Ax−x0=By−y0 , где (А;B) - направляющий вектор перпендикулярной прямой АВ.
(-3;1) - направляющий вектор.
\begin{gathered}\displaystyle \frac{x-6}{-3} = \frac{y-1}{1}\\ \\ \boxed{3y+x-9=0} \end{gathered}−3x−6=1y−13y+x−9=0
3) Уравнение медианы АМ.
Координаты точки М найдем по формулам деления отрезка пополам
x= \frac{1+6}{2} = \frac{7}{2} ;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,y= \frac{6+1}{2} = \frac{7}{2}x=21+6=27;y=26+1=27
M(\frac{7}{2} ;\frac{7}{2} )M(27;27) - точка М.
Уравнение медианы АМ будем искать по формуле для уравнение прямой, проходящей через две заданные точки.
\begin{gathered} \dfrac{x+2}{\frac{7}{2} +3} = \dfrac{y+3}{\frac{7}{2} +3} \\ \\ \\ \boxed{11y-13x+7=0}\end{gathered}27+3x+2=27+3y+311y−13x+7=0
4) Точку пересечения медианы АМ и высоты СН
\begin{gathered}\displaystyle \left \{ {{3y+x-9=0} \atop {11y-13x+7=0}} \right. \Rightarrow \left \{ {{x=9-3y} \atop {11y-13(9-3y)+7=0}} \right. \\ \\11y-117+39y+7=0\\ \\ 50y=110\\ y=2.2\\ x=2.4\end{gathered}{11y−13x+7=03y+x−9=0⇒{11y−13(9−3y)+7=0x=9−3y11y−117+39y+7=050y=110y=2.2x=2.4
N(2.4;2.2) - точка пересечения