Ну ты просто переносишь слагаемые из одной части неравенства в другую, поменяв при этом его знак на проивоположный, но не меняв знак неравенства. решу это неравенство.
- 4x² + 8x + 28 ≤ x² - 6x + 9
Переносим, получаем как бы вот это:
(-4x² - x²) + (8x + 6x) ≤ 9 - 28
-5x² + 14x ≤ -19
-5x² + 14x + 19 ≤ 0
5x² - 14x - 19 ≥ 0
решу неравенство методом интервалов:
5x² - 14x - 19 = 0
D = b² - 4ac = 196 + 380 = 576
x1 = (14 - 24) / 10 = -10/10 = -1
x2 = (14 + 24) / 10 = 38/10 = 3.8
Следовательно, разложение имеет вид:
5(x + 1)(x - 3.8) ≥ 0
(x+1)(x-3.8) ≥ 0
нанесу на прямую нули этой функции и найду нужные промежутки. результат:
(-∞;-1] и [3.8;+∞) - это ответ.
Для оценки снизу(что больше 30) мы берём интеграл функции 1/√х, т.е. 2√х. Возьмём его в промежутке от 256 до 1, значение равно 30(2*(√256-√1)) и является огранием снизу.(очевидно, что это ограничение именно снизу, т.к. сумма ряда-сумма площадей прямоугольников, содержащих в себе всю площадь интеграла)
Теперь найдём некоторую функцию, которая будет содержать в себе всю площадь этих самых прямоугольников:
Докажем, что 1/sqrt(2) +1/sqrt(3) +...+1/sqrt(256)<30. Возьмём функцию 1/√(х-1). В промежутке от х=2 до х=257 лежит целиком вся площадь рассмотриваемых прямоугольников. Т.е. интеграл этой функции на этом промежутке может служить верхней границей: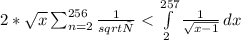 
. Тогда его значение на промежутке равно 30(=2*(√(257-1)-√(2-1))), а т. к. границы площадей прямоугольников и функции не совпадают, но все прямоуг. лежат под графиком, то 1/sqrt(2) +1/sqrt(3) +...+1/sqrt(256)<30(строго меньше), а значит 1+1/sqrt(2) +1/sqrt(3) +...+1/sqrt(256)<31
Тогда, т.к. 30<1+1/sqrt(2) +1/sqrt(3) +...+1/sqrt(256)<31, то целая часть этого ряда равна 30
ответ:30.
P.S. Площадью графика я называл площадь под графиком, которая считается равной значению определённого интеграла на этом участке.
