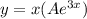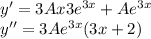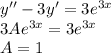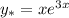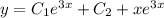1. у=8х-3
1). х=2: 8*2-3=13
2). 8х-3=19
8х=19+3
8х=22 |:8
х=2,75
3). В(-2;-13)
Подставляем: 8*(-2)-3=-19
-19≠-13
ответ: не проходит.
2. Смотри рисунок
1). у=1
2). х=3
3). -2х+5<0
-2х<-5 |:2
х>5/2
х>2,5
3. Приравниваем их:
47х-9=-13х+231
47х+13х=231+9
60х=240 |:60
х=4
Теперь считаем у: 47*4-9=179
(4;179)
5. у=-0,8х+4
С осью Ох (у=0): -0,8х+4=0
-0,8х=-4 |: (-0,8)
х=5
(5;0)
С осью Оу (х=0): -0,8*0+4=0+4=4
(0;4)
6. Чтобы две прямые были паралельны, нужно чтобы угловые коэффициенты были одинаковы. В данном случае это -5. y=-5x+b.
8=-5*(-2)+b, 8=10+b, b=-2, у=-5х-2.
.
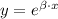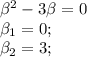
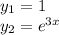
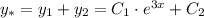
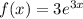
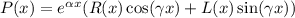, где R(x) и S(x) - полиномы, которое имеет частное решение.
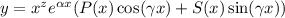, где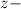 
кратность корня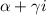 
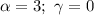
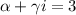является корнем характеристического уравнения кратности z=1
