1. Всего карточек 50 из них 9; 18; 27; 36; 45 кратны 9 - их всего 5 карточек.
Всего все возможных событий: n=50
Всего благоприятных событий: m = 5
Искомая вероятность: P = m/n = 5/50 = 1/10 = 0,1.
2. Всего все возможных подбрасывания игральных кубиков: 6*6=36
На желтой кости выпало четное число: {2;4;6}
На красной кости - {5}
Всего благоприятных событий: 3*1 = 3.
Искомая вероятность: P = 3/36 = 1/12
3. Вероятность того, что вынутая наугад карта окажется шестеркой красной масти равна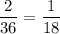 
. Тогда вероятность того, что вынутая наугад карта окажется не шестеркой красной масти равна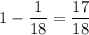 
4. Выпишем все выпадения очков, в сумме не меньше 11.
{6;6}, {5;6}, {6;5} - всего 3
Искомая вероятность: P = 3/36 = 1/12
5. Всего все возможных событий: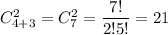 
Один красный шар можно достать а один белый По правилу произведения, достать один красный и один белый шары можно
Искомая вероятность: P = 12/21 = 4/7
Объяснение:
1) (a-5)(a+3) < (a+1)(a-7)
a^2-5a+3a-15 < a^2+a-7a-7
-2a-15 < - 6a-7
4a < 8
a < 2
Это неравенство верно вовсе не при любых а, а только при а меньше 2.
2) [5x+2] <= 3
Видимо, квадратные скобки это модуль. Неравенство распадается на два:
а) 5x+2 >= - 3
5x >= - 5
x >= - 1
б) 5x+2 <= 3
5x <= 1
x <= 1/5
Целые решения: - 1; 0
3) Пусть одна сторона равна 5 см, а другая больше неё в 4 раза, то есть 20 см.
Тогда периметр равен 2*(5+20) = 2*25 = 50 см.
Если первая сторона меньше 5 см, то вторая меньше 20 см, а периметр меньше 50 см.
