Задача. Пифагор на вопросы о числе учеников, посещающих его школу, ответил по преданию так: "Половина учеников изучает математику, четверть музыку, седьмая часть пребывает молчании. Остальную часть составляют 3 девы. Сколько было учеников у Пифагора.
Пусть х - количество учеников.
Тогда математику изучают х/2 учеников, х/4 изучают музыку , х/7 пребывает в молчании , остальные 3 человека - девы.
Составим уравнение .
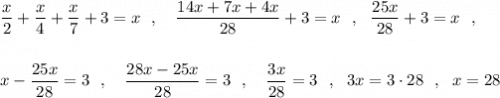
ответ: 28 учеников было у Пифагора .
P.S. У вас описка в условии. Не 5 женщин, а 3 по преданию. Если будет 5, то уравнение будет иметь вид 3х=140, и при делении 140 на 3 не получим целое число х .
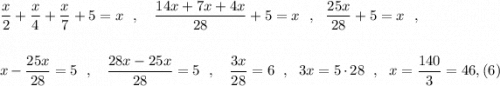
Не может количество человек быть дробным числом , значит описка в условии .
Перепишем первое уравнение в виде: x + y = -3
Система теперь выглядит так:
x + y = -3
x² + y² = 5
Это чисто метод замены переменной. Пусть x + y = a, xy = b.
Выразим x² + y² через a и b.
(x + y)² = x² + 2xy + y², с учётом замены
a² = x² + 2b + y², откуда
x² + y² = a² - 2b.
Идём далее, с учётом замены перепишем уже систему в следующем виде:
a = -3 a = -3 a = -3
a² - 2b = 5 2b = a² - 5 = 9 - 5 = 4 b = 2
Возвращаемся к старым переменным, учитывая, что x + y = a, xy = b
x + y = -3 y = -3 - x
xy = 2 x(-3-x) = 2 (1)
(1)-3x - x² = 2
x² + 3x + 2 = 0
x1 = -2; x2 = -1
Приходим к двум вариантам:
x = -2 или x = -1
y = -1 y = -2
Система решена