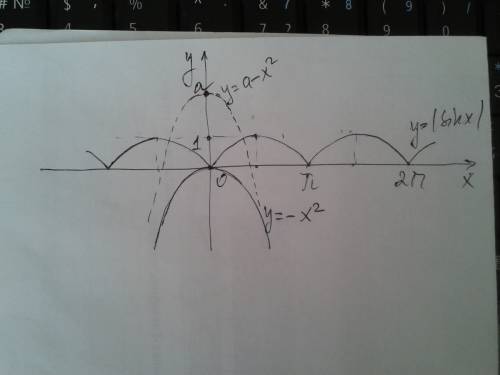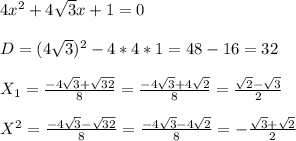
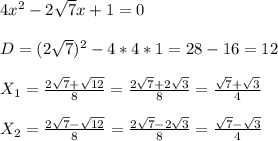
ответ: ниа.
объяснение:
к сожалению, не существует общего единого метода, следуя которому можно было бы решить любое уравнение, в котором участвуют тригонометрические функции. успех здесь могут обеспечить лишь хорошие знания формул и умение видеть те или иные полезные комбинации, что вырабатывается лишь практикой.
общая цель обычно состоит в преобразовании входящего в уравнение тригонометрического выражения к такому виду, чтобы корни находились из так называемых простейших уравнений:
сos px = a; sin gx = b; tg kx = c; ctg tx = d.
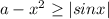
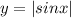 расположен выше оси ОХ.
расположен выше оси ОХ. 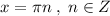 .
.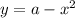 - это параболы , ветви
- это параболы , ветви