Чтобы оценить периметр исходного треугольника, нужно сложить заданные неравенства
2,3 ≤ a ≤ 2,4
3,2 ≤ в ≤ 3,3
4,5 ≤ c ≤ 4,6
2,3+3,2+4,5 ≤ a+в+с ≤ 2,4+3,3+4,6
10 ≤ P ≤ 10,3
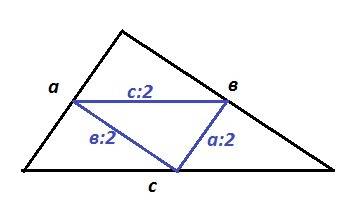
Соединили середины сторон, то есть провели 3 средние линии треугольника. Каждая средняя линия равна половине стороны, которой параллельна. Значит, периметр образованного треугольника равен половине периметра исходного треугольника
10 ≤ P ≤ 10,3 | : 2
10:2 ≤ P:2 ≤ 10,3 :2
5 ≤ P₁ ≤ 5,15
ответ : периметр полученного треугольника в пределах от 5 см до 5,15 см включительно.
или
y = x^2 - 8 и y = - х + 4
если графики пересекаются, то они имеют хотя бы одну общую точку.
х² - 8 = -х +4
х² +х -12 = 0
По т. Виета корни - 4 и 3
Т.е. х₁ = -4 и х₂ = 3
у₁ = -х +4 = 4 +4 = 8 и у₂ = -х +4 = -3 +4 = 1
Вывод парабола и прямая пересекаются в точках (-4; 8) и (3; 1)