В решении.
Объяснение:
Дві конкуруючі фірми, працюючи одночасно, поставили в місто певну кількість товару за 4 дні. За скільки днів може виконати цей же об'єм товаропостачання кожна фірма окремо, якщо фірма, що є технічним лідером може зробити це швидше на 6 днів, ніж друга.
Две конкурирующие фирмы, работая одновременно, поставили в город определенное количество товара за 4 дня. За сколько дней может выполнить этот же объем товароснабжения каждая фирма отдельно, если фирма, которая является техническим лидером, может сделать это быстрее на 6 дней, чем другая.
х - объём товара в день первой фирмы.
у - объём товара в день второй фирмы.
1 - весь товар.
1/х - дней потребуется первой фирме.
1/у - дней потребуется второй фирме.
По условию задачи система уравнений:
(х + у) * 4 = 1
1/х - 1/у = 6
Выразить х через у в первом уравнении:
(х + у) * 4 = 1
Разделить обе части на 4 для упрощения:
х + у = 0,25
х = 0,25 - у;
Преобразовать второе уравнение.
Умножить обе части на ху, чтобы избавиться от дроби:
1/х - 1/у = 6
у - х = 6ху
Подставить в уравнение выражение х через у:
у - (0,25 - у) = 6у(0,25 - у)
у - 0,25 + у = 1,5у - 6у²
6у² - 1,5у + 2у - 0,25 = 0
6у² + 0,5у - 0,25 = 0, квадратное уравнение, ищем корни:
D=b²-4ac = 0,25 + 6 = 6,25 √D=2,5
у₁=(-b-√D)/2a
у₁=(-0,5-2,5)/12 = -3/12, отбрасываем, как отрицательный.
у₂=(-b+√D)/2a
у₂=(-0,5+2,5)/12
у₂=2/12
у₂=1/6 - объём товара в день второй фирмы.
х = 0,25 - у
х = 1/4 - 1/6
х = 1/12 - объём товара в день первой фирмы.
1 : 1/12 = 12 - дней потребуется первой фирме.
1 : 1/6 = 6 - дней потребуется второй фирме.
Разница 6 дней, верно.
Решать такое надо графически.
Построим графики уравнений f(x,y)=0 (к 1-му неравенству); g(x,y)=0 (ко 2-му неравенству)
В 1-м неравенстве видно, что это эллипс.
Приведу его к каноническому виду:
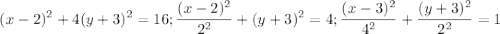
Это значит, что центр эллипса в точке (2;-3), по x он растянется максимум на 4 единицы, по у на 2.
Во 2-м видно, что будут 2 прямые.
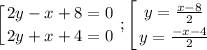
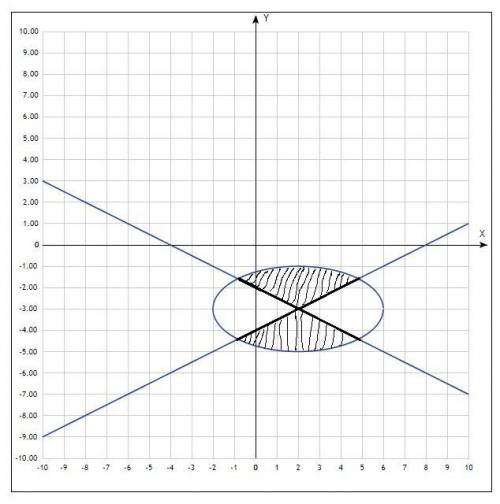
Построили графики на одной системе координат.
1-е неравенство говорит нам, что это геометрическое место точек, которые находятся ВНУТРИ эллипса, причем не захватывая его контур.
Теперь ко 2-му неравенству.
Прямые пересекаются (у них разные угловые коэффициенты) и образуют перекрестие, деля плоскость на 4 части. Нам будут нужны 2 части, это верхняя часть и нижняя, можно это проверить, подставив точку (0;0) во 2-е неравенство и (0;-5).
Получаются два сектора, причем прямые в них включатся в зону, так как 2-е неравенство системы нестрогое, а вот контуры эллипса как бы выколоты. Штриховкой я отметил нужную область.