Объяснение:
y-2x<-4
y<2x-4
y=2x-4 - линейная функция, график прямая
х | 0 | 2
у | -4 | 0
неравенство строгое, => прямая пунктирная(не включена, точки прямой не являются решением неравенства)
прямая делит координатную плоскость на две полуплоскости.
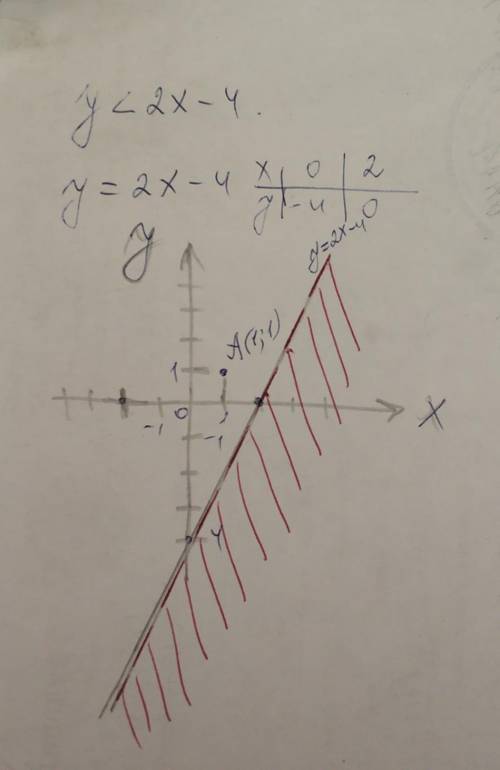
выберем произвольную точку А(1;1), координаты точки А подставим в неравенство:
1<2×1-4
1<-2 ложно,
=> точка А(1;1) и все точки лежащие с ней в одной полуплоскости не являются решением неравенства.
смотри вложение(решение - штриховка красным цветом
cos(5x)-cos(9x)+√(3)*sin(2x)=0
-2sin((5x+9x)/2)*sin((5x-9x)/2)+√3*sin(2x)=0
-2sin(7x)*sin(-2x)+√3*sin(2x)=0
2sin(7x)*sin(2x)+√3*sin(2x)=0
sin(2x)*(2sin(7x)+√3)=0
a) sin(2x)=0
2x=pi*n
x=pi*n/2
б) 2sin(7x)+√3=0
2sin(7x)=-√3
sin(7x)=-√3/2
7x=2*pi/3+pi*n
x=(-1)^n*4*pi/21 +pi*n/7
На проможутке [0; pi/3] находятся корни
0;
4*pi/21
- 4*pi/21 +3*pi/7