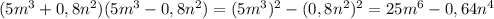
Cos 11pi / 6 = sqrt(3)/2
это 4 четверть значит меняем функцию ; угол меняем на три четверти уменьшаем. знак косинуса зависит от х0 (смотри чертёж) x0>0 оставляем .
3/4три четверти*2pi от полного оборота=6pi/4=9pi/6
Cos 11pi / 6= sin (11 pi - 9 pi )/6=sin(2pi/3) это вторая четверть значит меняем функцию на косинус и отнимаем одну четверть знак синуса зависит от y0 (смотри чертёж) y0>0 оставляем
1/4одна четверть*2pi от полного оборота=2pi/4=1pi/2=3pi/6
cos(2pi/3-3pi/6)=cos(pi/6) это табличное значение = sqrt(3)/2
Cos 11pi / 6 = sqrt(3)/2
По аналогии дальше ....
2 и 4 четверть меняем функцию , 1 и 3 четверть оставляем . знак зависит от функции если синус то смотри чертёж и Y0 ну а если косинус то смотри X0
Sin 23pi /6 = -1/2
sin 5pi/3 = -sqrt(3)/2
cos 7pi/4 = sqrt(2)/2
tg -19pi/3 = -sqrt(3)
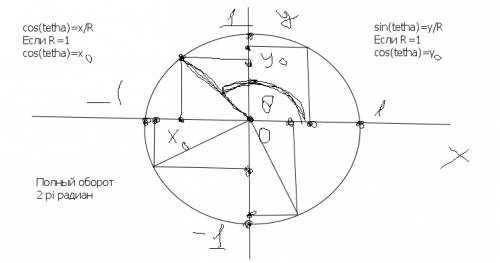
Для определения значения тригонометрической функции, найдите его на пересечении строки с указанием тригонометрической функции. Например, синус 30 градусов - ищем колонку с заголовком sin (синус) и находим пересечение этой колонки таблицы со строкой "30 градусов", на их пересечении считываем результат - одна вторая. Аналогично находим косинус 60 градусов, синус 60 градусов (еще раз, в пересечении колонки sin (синус) и строки 60 градусов находим значение sin 60 = √3/2 ) и т.д. Точно так же находятся значения синусов, косинусов и тангенсов других "популярных" углов.
Объяснение:
Arcsin(ctg(π/4))=arcsin(1)=π/ 2 cos(arcsin(-1/2)-arcsin(1))=cos(2π/3-π/2)= cos(4π/6-3π/6)=cos(π/6)=√3/2.