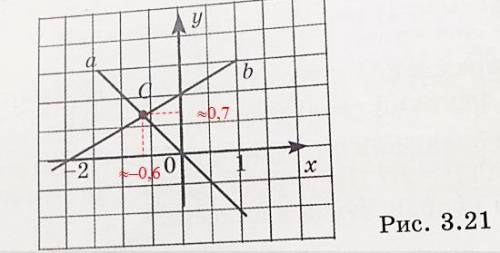
Не хватающий рисунок 3.21 в приложении.
1. Прямая a проходит через точки (0; 0) и (1; –1). Подставляем эти координаты в общее уравнение прямой с угловым коэффициентом y=k•x+m:
(0; 0): 0=k•0+m, то есть m=0, тогда уравнение прямой принимает вид y=k•x,
(1; –1): –1 = 1•k и отсюда k=–1.
Значит, уравнение прямой имеет вид: y = –x.
2. Прямая b проходит через точки (0; 1) и (–2; 0). Подставляем эти координаты в общее уравнение прямой с угловым коэффициентом y=k•x+m:
(0; 1): 1=k•0+m, то есть m=1, тогда уравнение прямой принимает вид y=k•x+1,
(–2; 0): 0 = –2•k+1 и отсюда k=0,5.
Значит, уравнение прямой имеет вид: y = 0,5•x+1.
3. По рисунку видно, что приближенные значения координат точки С(–0,6; 0,7).
Проверим точность аналитическим то есть находим точку пересечения прямых a и b:
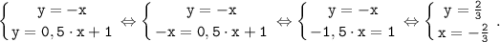
Так как 2/3=0,666..., то приближённые значения совпадают с точностью 10⁻¹.
Их произведение равно 117.
х*(х-4) = 117
Раскроем скобки
х^2-4х = 117
Перенесём 117, знак меняется
х^2-4х-117 = 0
Решаем квадратное уравнение
a=1; b=(-4); c=(-117)
D = (-4)^2-4*(-117) = 484 = 22^2
x1 = 4+22/2 = 13
x2 = 4-22/2 = -9 - этот корень не берём, т.к. получится отрицательное число.
Итак, х=13 - второе число, тогда 13-4=9 - первое.
13*9 = 117.
ответ: первое число - 9, второе - 13.