Значение выражения
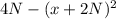
наибольшее при значении

При
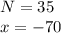
значение выражения равно
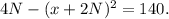
Объяснение:
Обозначим за a значение выражения, данное в условии:
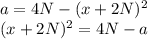
Для любых значений х и N левая часть равенства не может быть отрицательной, т.к. в ней выражение возведено в квадрат.
Соответственно, правая часть равенства тоже должна быть более или равна нулю:
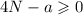
Отсюда можно выразить искомое а
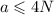
Соответственно, максимальное значение, которое может принять наше выражение, равно 4N
(по сути, это значение выражения, когда под квадратом ноль)
Подставим 4N в начальную формулу
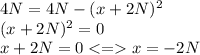
При значениях N = 35 получаем
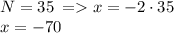
А значение выражения равно:
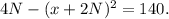
972 или 871
Объяснение:
пусть
x записано в виде abc, то есть
x=100a+10b+c
(а,b,c -натуральные от 1 до 9 или 0)
тогда по условию
100a+10b+c -( 100c+10b+a)=693
a+b+c=18
из первого получим
99a-99c=693
или
a-c=7
так как a и с могут принимать только целые неотрицательные значения от 0 до 9
то мы получаем следующие пары
а1=9 с1=2
а2=8 с2=1
а3=7 с3=0
теперь вспоминаем про второе условие
а+b+c=18
b=18-a-c
третий вариант не подходит, так как
b3=11
поэтому остаются следующие
а1=9 b1=7 с1=2
а2=8 b1=9 с2=1
откуда наше число
x1=972
или х2=891
2.
3.
_______________________________
1. (5 - x)² - x(2,5 + x) = 0
25 - 10x + x² - 2,5x - x² = 0
-10x - 2,5x = -25
-12,5x = -25
x = -25 / 12,5
x = 2
ответ: x = 2
________________________
2.