Пусть C — первая деталь окажется стандартной. Гипотезы:
H₁ - деталь изготовлена первым заводом;
H₂ - деталь изготовлена вторым заводом;
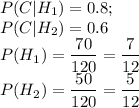
Вероятность события А по формуле полной вероятности
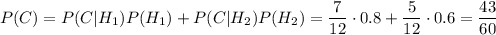
По формуле Байеса, вероятность того, что эта деталь изготовлена первым заводом, равна:
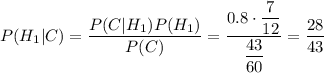
Аналогично, пусть В — вторая деталь окажется стандартной. Так как одна деталь уже вынута, то в партии остается 119 лампочек, из них 69 изготовлены на первом заводе.
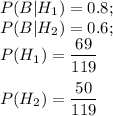
По формуле полной вероятности, вероятность события В:
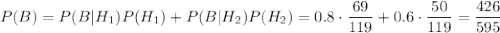
По формуле Байеса, вероятность того, что эта деталь изготовлена первым заводом, равна:
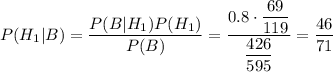
По теореме умножения, вероятность того, что наудачу взятые две лампочки являются стандартными, равна
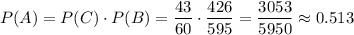
По теореме умножения, вероятность того, что обе лампочки изготовлены на первом заводе, при условии что событие А произошло, равна:
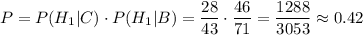
а) 3, 6, 9, 12, 15
б) а6=18
в) число 19 - простое, поэтому не делится на 3, значит, его нет в последовательности
число 27 есть в последовательности, т.к. оно делится на 3.
2.
х1 = -5 d = 2
xn=x1+(n-1)*d
x6=-5+4*2=3
x11=-5+10*2=15
3.
а10 =13, d=5
an=a1+(n-1)*d
a1=an-(n-1)*d
a1=a10-9*d=13-9*5=13-45=-32
4.
a1=-14 a2=-6 a3=2
d=a3-a2=2+6=8
an=a1+(n-1)*d
an=-14+(n-1)*8
-14+(n-1)*8>800
(n-1)*8>814
n-1>814/8
n>407/4+1
n>102,75
Начиная с n=103 члены арифметической прогрессии будут больше 800.