(см. объяснение)
Объяснение:
Заметим, что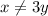 
. Пусть 
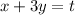. Тогда из первой строки получим, что 
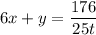. Подставив это во вторую строку системы, получим 
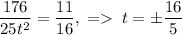. Тогда получим систему, которая будет состоять из строк 
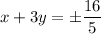и 
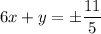. Решая две полученные системы уравнений, находим, что исходная система уравнений имеет две пары решений вида 
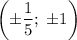. Тогда окончательным ответом с учетом ОДЗ будет: 
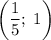или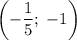 
.
Система уравнений решена!
Комментарий-1:
При решении несложно было заметить, что из второй строки системы следует, что y=5x.
Комментарий-2:
При выполнении замены, можно было указать, что 6x+y=t и проделать аналогичную в решении работу.
ответ: 7.
Объяснение:
Смотри первое приложение. Закрасим 7 клеток чтобы выполнялось условие (лев. квадрат 5х5). Докажем, что меньше семи клеток быть не может (прав. квадрат 5х5). Рассмотрим два квадрата 3х3 (красн. и син.). Чтобы количество закрашенных клеток было минимальным, необходимо закрасить все общие клетки этих квадратов (1 центральная). Видим, что для двух этих квадратов необходимо закрасить ещё по 3 клетки, чтобы всего было по 4. Тогда минимальное количество клеток 1+3+3=7, что и требовалось доказать. Во втором приложении я рассмотрел каждый квадрат 3х3, чтобы показать правильность расстановки.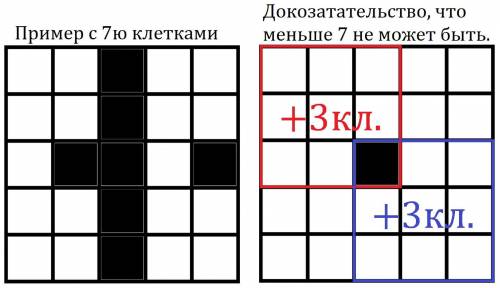
х/190*100% - концентрация изначального раствора
(х+10)/200*100% - концентрация нового раствора
(х+10)/200*100%=х/190*100%+4,5%
(х+10)/2=10х/19+4,5 *38
19(х+10)=2*10х+171
19х+190=20х+171
х=190-171=19
19 г соли изначально было в растворе