 .
. .
. .
.
 . Но
. Но  фактически лишнее неравенство, оно выполняется автоматически потому, что
фактически лишнее неравенство, оно выполняется автоматически потому, что 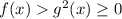 , ибо полный квадрат всегда неотрицателен.
, ибо полный квадрат всегда неотрицателен.
 .
. .
. .
.
 . Но
. Но  фактически лишнее неравенство, оно выполняется автоматически потому, что
фактически лишнее неравенство, оно выполняется автоматически потому, что 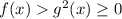 , ибо полный квадрат всегда неотрицателен.
, ибо полный квадрат всегда неотрицателен.
Воспользуемся формулой понижения степеней.
Решая как квадратное уравнение относительно cos2x, получим