Вариант 2.
Задание 1.
1.
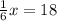
х = 18 : 
х = 18 * 6
х = 108
2.
7х + 11,9 = 0
7х = -11,9
х = -11,9 : 7
х = -1,7
3.
6х - 0,8 = 3х + 2,2
6х - 3х = 2,2 + 0,8
3х = 3
х = 3 : 3
х = 1
4.
5х - (7х + 7) = 9
5х - 7х - 7 = 9
-2х = 9 + 7
-2х = 16
х = 16 : (-2)
х = -8
Задание 2.
х км - на автобусе
9х км - на самолете
Составляем уравнение:
х + 9х = 600
10х = 600
х = 600 : 10
х = 60
60 км - на автобусе .
ответ: 60 км.
Задание 3.
Допустим на другом участке было х саженцев, тогда на первом - 5х .
После перевоза получилось:
х + 90 - другой участок.
5х - 50 - первый участок.
Составляем уравнение:
5х - 50 = х + 90
5х - х = 90 + 50
4х = 140
х = 140:4
х = 35
35 саженцев - на другом участке первоначально.
35 * 5 = 175 саженцев - было на первом участке первоначально.
ответ: 175, 35.
Задание 4.
6х - (2х - 5) = 2(2х + 4)
6х - 2х + 5 = 4х + 8
6х - 2х - 4х = 8 - 5
0х = 3
Нет решения.
Дана функцию f(x) = (x² - 3x) / (x - 4 ).
1 ) Найдите наибольшее и наименьшее значения функции на данном промежутке [-1; 3].
2 ) Найдите промежутки возрастания и убывания и точки экстремума функции .
ответ: 1 ) наибольшее 1 ; наименьшее - 0,8 .
2 )
Функция возрастает: x ∈( -∞ ; 2 ] и x ∈[ 6 ;∞) .
Функция убывает x∈[2 ; 4) и x ∈(4 ;6] ;
Точки экстремумов: x =2 точка максимума и x = 6 точка минимума .
Объяснение: D(f) : ( - ∞ ; 4) ∪ (4 ; ∞ ) [ R \ {4 } ]
( u(x) /v(x) ) ' = ( u'(x)*v(x) - u(x)*v'(x) ) / v²(x)
f ' (x) = ( (x² - 3x) / (x - 4 ) ) ' =( (x² - 3x) ' *(x - 4 ) - (x² - 3x)*(x-4) ' ) / (x-4)² =
( (2x - 3)*(x - 4 ) - (x² - 3x)* 1 ) / (x-4)² = (x² - 8x +12) / (x-4)² =(x-2)(x-6) / (x-4)².
f ' (x) = 0 ⇔(x-2)(x-6) / (x-4)² =0 ⇒ x₁ =2 , x₂ = 6 .
f'(x) не существует в точке x =4 , но в этой точке не существует и функция
1)
* * * x₂ = 6 ∉ [ -1 ; 3 ] * * *
x₁=2 ∈ [ -1 ; 3 ] f (x₁ ) =f (2 ) =(2² -3*2) /(2 - 4) = 1 ;
f (a ) =f (-1 ) =( (-1)² -3*(-1) ) /( (-1) - 4) = - 4/5 = - 0,8 ;
f(b) = f(3) = (3² - 3*3) /(3 -4) = 0
На промежутке [-1;3] наибольшее значение функции равно 1 (если x=2 ), наименьшее значение -0,8 (если x= - 1 ) .
2)
Промежутки возрастания и убывания и точки экстремума функции .
f ' (x) = 0 ⇔(x-2)(x-6) / (x-4)² =0 ⇒ x₁ =2 , x₂ = 6 .
Функция возрастает , если f ' (x) ≥ 0
Функция убывает , если f ' (x) ≤ 0
По методу интервалов
f '(x ) + + + + + + + + + + [ 2 ] - - - - - - - - - - [ 6] + + + + + + +
f (x ) ↑ (возрастает) ↓ (убввает) ↑ (возрастает)
Функция возрастает: x ∈( -∞ ; 2 ] и x ∈[ 6 ;∞) .
Функция убывает x∈[2 ; 4) и x ∈(4 ;6] .
x =2 и x=6 точки экстремумов ( производная функции меняет знак при прохождения через эти точки )
x =2 точка максимума , f(2) = 1
x =6 точка минимума , f(6)=(6² -3*6) /(6 - 4) =(36-18)/ 2=9.
9 *(8/3)^2+b(8/3)+80=0; 64+8/3b+80=0
8/3b= -144
b= -54
теперь значение b подставим в уравнение,получим
9x^2-54x+80=0 решим это уравнение и найдем второй корень
D/4=(-54/2)^2-80*9=729-720=9
x1=(27-3)/9=8/3=2 2/3
x2=(27+3)/9=3 1/3
ответ: второй корень равен 3 1/3