 ,
, , a
, a 
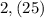
 целая часть. У нас она равна 2
целая часть. У нас она равна 2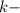 - количество цифр в периоде. У нас их 2
- количество цифр в периоде. У нас их 2 количество цифр до периода. У нас их 0
количество цифр до периода. У нас их 0 все цифры, включая период, в виде натурального числа. У нас это 25
все цифры, включая период, в виде натурального числа. У нас это 25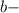 все цифры без периода в виде натурального числа. Их нет.
все цифры без периода в виде натурального числа. Их нет.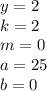
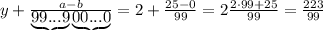
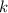 подставляется количество 9, а под
подставляется количество 9, а под  -количество нулей. У нас
-количество нулей. У нас 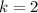 , значит пишем две цифры 9, а
, значит пишем две цифры 9, а  , значит, нулей не пишем вообще. Между
, значит, нулей не пишем вообще. Между 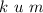 не стоит знак умножения
не стоит знак умножения
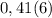

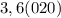

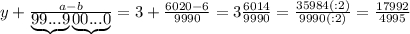
3x^2-8x+6=0
D=b2-4ac=64-72= -8
нет корней
2)6-3x^2=8x
-3x^2-8x+6=0
D=64+72=136
x1=-2b+кореньD/2a=16+2корня из34/-6
x2=2b-кореньD/2a=16-2корня из34/-6
3)7x=6x^2-5
6x^2-7x-5=0
D=49+120=169
корень169=13
x1=14+13/12=27/12=9/4=2,25
x2=13-13/12=1/12
4)(x+9)(5x-6)=0
5x^2-6x+45x-54=0
5x^2+39x-54=0
D=1521+1080=2601
корень 2601=51
x1=-78+51/10=-2,7
x2=-78-51/10=-12,9
5)(2x+5)^2-2(2x+9)=0
4x^2+20x+25-4x-18=0
4x^2+16x+7=0
D=256-112=144
корень 144=12
x1=-32+12/8=-20/8= -2,2
x2=-32-12/8= - 44/8= -5,5