Так как в уравнении есть квадратные корни, то запишем ОДЗ:
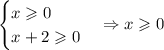
Также заметим, что в левой части записано произведение двух неотрицательных выражений. Значит, правая часть уравнения также неотрицательна:
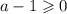
Таким образом, при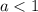 
уравнение не имеет корней.
Предположим, что . Тогда:
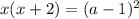
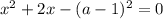
Проверим, удовлетворяют ли найденные корни ОДЗ.
Для первого корня получим:
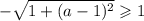
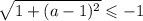
Однако, квадратный корень не может принимать отрицательных значений. Значит, рассматриваемое выражение не является корнем уравнения ни при каких значениях параметра 
.
Для второго корня получим:
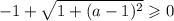
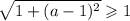
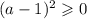
Последнее условие выполняется при любых значениях параметра . Но как отмечалось ранее, уравнение может иметь корни только при . Значит, данное выражение является корнем уравнения при .
при 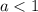: нет корней,
при : 
Обозначим за X скорость лодки при гребле в стоячей воде, а за Y - скорость течения.
Тогда очевидно, что изначально она плыли 1 час со скоростью (X+Y), затем они не гребли т.е. лодка плыла со скоростью течения Y 30 минут(0.5 часа), а после всего этого они возвращались на старт т.к. плыли обратно против течения 3 часа со скоростью (X-Y).
Составим простое уравнение
(X+Y)+0.5*Y=3*(X-Y)
Упростим его:
X+1.5*Y=3*X-3*Y
2*X=4.5*Y
разделим обе части на меньший коэффициент:
X=2.25*Y
Отсюда следует, что скорость течения реки в 2.25 раз меньше собственной скорости лодки.
d(4,8d^2+6,4d)