1) 8 < 2x+y < 30
2) 6 < xy < 48
3) -3 < x-y < 6
Объяснение:
3 < x < 8
2 < y < 6
1) 2x+y
сначала вычислим минимальный предел:
2*3+2=8;
затем максимальный:
8*3+6=30.
Получится 8 < 2x+y < 30
2) xy
сначала вычислим минимальный предел:
3*2=6;
затем максимальный:
8*6=48.
Получится 6 < xy < 48
3) x-y
Так как здесь присутствует вычитание. Сначала из меньшего значения x вычитаем большее значение y, так мы получим минимальный предел выражения x-y. Потом из большего значения x вычитаем меньшее значение y, так мы получим максимальный предел значения x-y.
сначала вычислим минимальный предел:
3-6=-3;
затем максимальный:
8-2=6.
Получится -3 < x-y < 6
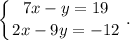
Выразим в первом уравнении переменную "у". Для этого нужно перенести неизвестную в правую часть и сменить ее знак. Получим:
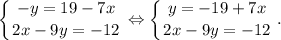
Подставим данное значение "у" в уравнение "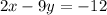
". Получим:
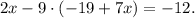
Рапределяем "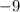
" через скобки. Получим:
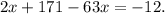
Приводим подобные члены. Получим:
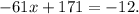
Переносим постоянную в правую часть и сменяем ее знак. Получим:
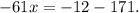
Вычисляем разность. Получим:
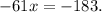
Делим обе стороны уравнения на "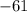
". Получим:
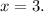
Подставляем данное значение "х" в уравнение "у=-19+7х". Получим:
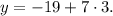
Умножаем числа. Получим:
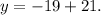
Вычисляем сумму. Получим:
" 
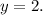
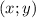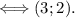
5(y+2)(y+3)=5(y²+3y+2y+6)=5y²+15y+10y+30=5y²+25y+30
-6a(a+4)(a-1)=-6a(a²-1a+4a-4)=6a³-6a²+24a²-24a=6a³-18a²-25-24a
(2a-3)(5a+7)+21=10a²+14a-15a-21+21=10a²-1
(x+4)x-(x-3)(x+7)=x+4x+x²+7x-3x-21=9x+x²-21