 — общее число человек на экзамене по математике.
— общее число человек на экзамене по математике. ,
,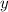 . Итак, число верно решивших относится к числу не решивших вовсе, как 5:3. Получается:
. Итак, число верно решивших относится к числу не решивших вовсе, как 5:3. Получается: 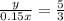 , отсюда
, отсюда 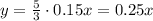 .
. , решили с ошибками 144, решили правильно
, решили с ошибками 144, решили правильно 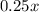 . Вместе эти три группы есть общее число человек на экзамене, то есть
. Вместе эти три группы есть общее число человек на экзамене, то есть  . Получаем:
. Получаем: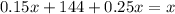
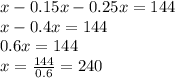
В первом и во втором десятках таких чесел нет, т.к. наибольшая сумма равна 1+ 9 = 10, что не больше 10. Во третьем десятке будет одно такое число 2 + 9 = 11. В четвёртом - уже 2 числа 3 + 8 = 11 и 3 + 9 = 12. В пятом - 3 числа 4 + 7 = 11, 4 + 8 = 12 и 4 + 9 = 13. Итого, 1 + 2 + 3 = 6
Вероятность того, что сумма цифр на карточке, вытащенной наугад, будет больше 10 равна:
Р = 6 / 50 = 3 / 25 = 0,12