1)найдите область определения выражения. √35+3x-2x² (числитель весь под корнем! ) x²-16 2)найдите сумму всех натуральных чисел, не превосходящих 120, которые не делятся на 3.
Чертим трапецию АВСД проводи одну диагональ ВД получается 2 равнобедренных треугольника АДВ и ВСД пусть α угол при основании треугольника который примыкает к верхнему основанию ∠СВД β ∠ВАД тогда из условий трап получаем ∠ВАД+∠АВС=180° β+(β+α)=α+2β=180° из треуг ВСД ∠ВСД=180°-2α=∠АВС=α+β решим систему уравнений α+2β=180° α=180°-2β α=180°-2β α=180°-2β α=180°-144° 180°-2α=α+β 3α+β=180° 3*180°-6β+β=180° 5β=360° β=72° α=36° α+β=36°+72°=108° тогда углы трапеции равны 72°, 108°, 108°, 72°
Чертим трапецию АВСД проводи одну диагональ ВД получается 2 равнобедренных треугольника АДВ и ВСД пусть α угол при основании треугольника который примыкает к верхнему основанию ∠СВД β ∠ВАД тогда из условий трап получаем ∠ВАД+∠АВС=180° β+(β+α)=α+2β=180° из треуг ВСД ∠ВСД=180°-2α=∠АВС=α+β решим систему уравнений α+2β=180° α=180°-2β α=180°-2β α=180°-2β α=180°-144° 180°-2α=α+β 3α+β=180° 3*180°-6β+β=180° 5β=360° β=72° α=36° α+β=36°+72°=108° тогда углы трапеции равны 72°, 108°, 108°, 72°
1) Выражение под корнем не может быть отрицательным, знаменатель не может быть равен нулю. То есть:
2) Сумма всех чисел от 1 до 120:
Числа, которые ДЕЛЯТСЯ на 3, образуют арифм. прогрессию с первым членом 3 и шагом 3 (3, 6, 9, 12 ... 120). Таких чисел всего 120/3 = 40. Их сумма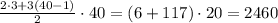
Тогда сумма чисел, которые НЕ делятся на 3 равна
7260-2460 = 4800