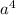 -6²+3)
-6²+3)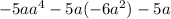 ·3
·3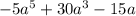
Объяснение:
Подставим координаты точки в каждое уравнение системы . Если получим верные числовые равенства, то данная пара является решением системы .
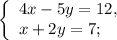
(-3;2) 4*(-3) -5*2 =12;
-12-10=12;
-22≠ 12
Подставлять во второе уравнение не имеет смысла
(-3;2) - не является решением системы.
(3; -2) 4*3-5*(-2)=12
12+10=12
22≠12
(3;-2) - не является решением системы.
(3;2) 4*3-5*2=12
12-10=12
2≠12
(3;2) - не является решением системы.
ответ: ни одна из данных пар чисел не является решением системы
Решим систему:
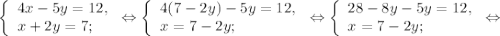
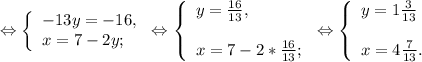
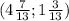 - решение данной системы. Значит ни одна из пар чисел не является решением системы.
- решение данной системы. Значит ни одна из пар чисел не является решением системы.
2)(x+4)(3x-2)=3x²-2x+12x-8=3x²+10x-8
3)(6m+5n)(7m-3n)=42m²-18mn+35mn-15n²-42m²+17mn-15n²