Объяснение:
если известно, что искомая прямая y₁ = k₁x +b₁ параллельна прямой y=-4x+51 (у=кх +b), то мы знаем коэффициент k₁ = -4 при x, т.к. у параллельных прямых коэффициенты k и к₁ при х равны.
тогда мы уже имеем "половину" уравнения у₁ = -4х +b₁
теперь для определения b₁ используем то, что искомая прямая проходит через точку M(-1; 3). это означает, что координаты точки должны удовлетворять уравнению у₁ = -4х +b₁. подставим эти координаты
3= -4*(-1) +b₁ тогда b₁ = -1
и искомое уравнение
у₁ = -4х -1
теперь проверим, принадлежит ли построенному графику точка N(-50; 200). подставим ее координаты в уравнение у₁ = -4х -1
200 ≠ -4*(-50)-1
точка N(-50; 200) ∉ графику функции у₁ = -4х -1
тогда строим график по двум точкам
х = -1 у₁(-1) = 3 точка M(-1; 3)
х = 0 у₁(0) = -1
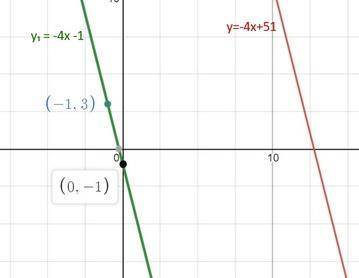
на первом фото построение по двум точкам у₁ = -4х -1 ║y=-4x+51
на втором показано, что точка N(-50; 200). ∉ графику у₁ = -4х -1
Если угол ромба равен 60 град., то односторонний с ним угол будет 120 град. Если провести диагональ из угла 120 град, то она разделит ромб на 2 равносторонних треугольника, так как эта диагональ разделит угол 120 град пополам и противоположный угол также. Следовательно, эта диагональ будет равна стороне ромба, а именно 12 см. Найдем высоту в равностороннем треугольнике по теореме Пифагора: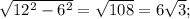 
см. Удвоенное это число дает длину второй диагонали:
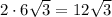см.
Найдем площадь ромба: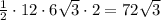 
см^2.
ответ: S=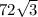
см^2; Малая диагональ равна 12см, большая диагональ равна 
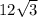см.
2 * 5 = 10 см . По условию периметр прямоугольника равен периметру
пятиугольника, значит тоже равен 10 см. У прямоугольника длина больше
ширины в 4 раза . Обозначим ширину через x , тогда длина 4x .
2(x + 4x) = 10
5x = 5
x = 1 см - ширина прямоугольника
4 * 1 = 4 см - длина прямоугольника
S = 1 * 4 = 4 см²