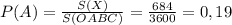
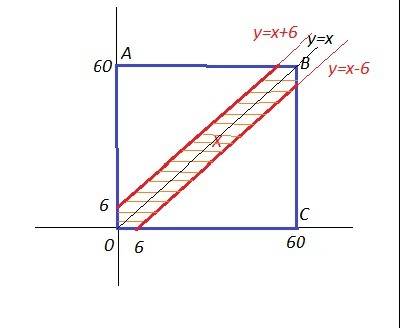
xy+x+y=11; {xy+x+y=11;
{x²y+xy²=30. ⇒ {xy(x+y)=30.
Пусть х+у=u; xy=v
{v+u=11;
{vu=30.
Решаем систему подстановки:
{v=11-u;
{(11-u)u=30.
Решаем второе уравнение системы
u²-11u+30=0
D=(-11)²-4·30=121-120=1
u₁=(11-1)/2=5 или u₂=(11+1)/2=6
v₁=11-u₁=11-5=6 или v₂=11-6=5
Обратная замена
{x+y=5 или {x+y=6
{xy=6 {xy=5
{y=5-x {y=6-x
{x(5-x)=6 {x(6-x)=5
Решаем вторые уравнения систем:
x²-5x+6=0 x²-6x+5=0
D=25-24=1 D=36-20=16
x₁=(5-1)/2=2; x₂=(5+1)/2=3 x₃=(6-4)/2=1; x₄=(6+4)/2=5
y₁=5-2=3; y₂=5-3=2 y₃=6-1=5; y₄=6-5=1
О т в е т. (2;3) (3;2) (1;5) (5;1).
Пустьх км/ч – скорость первого автомобилиста,
тогда (х + 54) км/ч - скорость второго автомобилиста
Время второго автомобиля, за которое он весь путь
0,5 / 36 + 0,5/(x + 54)
Время первого автомобиля равно времени второгоавтомобиля.
1/x = 0,5 / 36 + 0,5/(x +54)
1/x - 0,5/ 36 - 0,5/(x + 54) = 0
36(x + 54) – 0,5x(x + 54) – 0,5*36x = 0
36x +1944 – 0,5x² - 27x – 18x = 0
– 0,5x² - 9x + 1944 = 0 I :(-0.5)
x² + 18x –3888 = 0
D= 324 + 4*1*3888 = 15876 = 1262
X₁ = (- 18 – 126)/2 = - 72 неудовлетворяет условию задачи
X₂ = (- 18 + 126)/2 = 54
54км/ч - скорость первого автомобилиста
ответ: 54 км/ч