вероятность.
2. 10!
3. 26%
4. 1) 5/8 (от 6 до 9)
2) 1/36 (на грани первого — шесть, второго — пять)
3) 35/36 (хотя бы на одной грани не 6)
5. Нету количества троечников, поэтому задача нерешаема.
Объяснение:
1) После того, как нашли количество выбрать три согласных и количество выбрать одну гласную, умножаем первое на второе.
Чтобы найти вероятность составления слова "тест", сначала найдём количество комбинаций 6-и элементов по три и 5-ти элементов по 1. Далее находим вероятность найти определённую комбинацию 6-ти элементов по три и 5-ти по 1. Умножаем числа, что получили.
3) От "больше восьми" вычисляем "больше десяти" и получаем то, что искали.
4) 1) Рисуем квадрат с 36-ю квадратиками-исходами, внутри которых пишем количество очков на кубиках. Находим количество благоприятных исходов.
2) Правило умножения: P(A,B)=P(A)×P(B)=1/6*1/6=1/36
3) Условие будет не выполняться только тогда, когда на обоих кубиках будет 6. Вероятность этого — 1/36. Значит, вероятность выполнения условия — 1-1/36=35/36.
a < 0
Объяснение:
Когда мы видим уравнения с x и y в квадрате и с одинаковыми коэффициентами перед ними, это наводит на мысль, что перед нами уравнение окружности. Оно имеет вид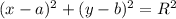 
. Попробуем преобразовать его к данному виду. Для этого нужно поделить обе части на 2, чтобы коэффициент при старших членах был 1, и выделить полные квадраты:
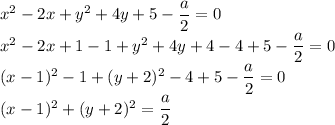
Это окружность с радиусом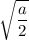 
. Если радиус равен нулю, то окружность превращается в точку. Значит, окружности не существует, если не выполняется ОДЗ корня: 
.
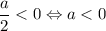Можно было рассуждать немного иначе: провести те же самые преобразования, но рассуждать не в терминах окружности, а в терминах суммы. В левой части сумма двух квадратов, каждый из них не меньше нуля. Значит, вся левая часть не меньше нуля, причём слагаемые друг от друга не зависят, поэтому в левой части можно представить любое неотрицательное число. Но тогда и правая часть не меньше нуля. Если же правая часть меньше нуля, то пара (x; y) не найдётся.
2)(x-5)×(x-1)×(x+1)