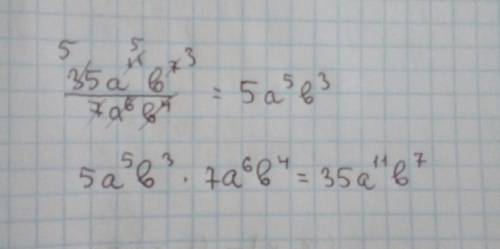
1) y = x2 + 2x - 3
График - парабола ( здесь так же указывается направление ветвей параболы. Если переменная a>0 - ветви вверх, если a<0 - ветви вниз. В нашем случае ветви у параболы направлены вверх 1>0 )
D (y): x - любое ( какая бы парабола не была - эта строка неизменна)
Вершина: ( -1; -4 ), т.к.
m ( x ) = -2:2 = -1
n ( y ) = (-1)2 +2(-1) - 3 = -4.
с осью OY: ( 0; -3 ), т.к.
y = 0x2 + 0*2 - 3
y = -3
с осью OX: ( -3; 0 ) и ( 1; 0 ), т.к.
x2 + 2x - 3 = 0
D = 4 - 4*1(-3) = 4 + 12 = 16
x1 = ( -2 - 4 ):2 = -3
x2 = ( -2 + 4 ):2 = 1.
Построим ещё две точки:
x = 2 y = 5
x = -2 y = -3.
Приклад:
Розв'язати систему рівнянь: {x−2y=3,5x+y=4.
1) З першого рівняння системи виражаємо змінну x через змінну y.
Отримуємо: x−2y=3,x=3+2y;
2) Підставимо отриманий вираз замість змінної x у друге рівняння системи:
5⋅x+y=4,5⋅(3+2y)+y=4;
3) Розв'яжемо утворене рівняння з однією змінною, знайдемо y:
5⋅(3+2y)+y=4,15+10y+y=4,10y+y=4−15,11y=−11,|:11y=−1¯¯¯¯¯¯¯¯¯¯¯.
4) Знайдемо відповідне значення змінної x, підставивши значення змінної y, у вираз знайдений на першому кроці:
x=3+2⋅y,x=3+2⋅(−1),x=3−2,x=1¯¯¯¯¯¯¯¯.
5) Відповідь: (1;−1) .
Объяснение:
это решить линейные уравнения без черчежей