Поскольку эта задача уже решалась совсем недавно, позволю себе опустить подробности. Дважды возводя в квадрат (второй раз - уединяя корень), получим уравнение
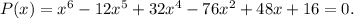
Сначала будем искать так называемые парные корни, то есть корни вида 
Такие корни ходят парами, дают в разложении скобку (x²-a^2). Для поиска таких корней надо решать систему из двух уравнений, приравнивая отдельно к нулю сумму четных степеней и сумму нечетных степеней. Доказательство этого факта я оставляю читателю. В нашем случае находим корни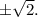 
Далее ищем кратные корни (они, как известно, ищутся из системы 
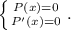В результате находится кратный корень 2 кратности 2. После деления остается квадратный трехчлен с конями 
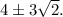Работу по выделению истинных корней оставляю читателю. ответ: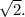 
На этом разрешите закончить это немного хулиганское решение.
Если кто-нибудь захочет услышать поподробнее про парные корни, составьте самостоятельно многочлен с парными корнями, приравняйте его к нулю и предложите мне решить такое уравнение. В этом случае я все внимание уделю этой теме.
Благоприятных случаев: ?
1*1 = 1 (<10)
1*2 = 2 (<10)
1*3 = 3 (<10)
1*4 = 4 (<10)
1*5 = 5 (<10)
1*6 = 6 (<10)
2*1 = 2 (<10)
2*2 = 4 (<10)
2*3 = 6 (<10)
2*4 = 8 (<10)
2*5 = 10 (=10)
2*6 = 12 (>10)
3*1 = 3 (<10)
3*2 = 6 (<10)
3*3 = 9 (<10)
3*4 = 12 (>10)
3*5 = 15 (>10)
3*6 = 18 (>10)
4*1 = 4 (<10)
4*2 = 8 (<10)
4*3 = 12 (>10)
4*4 = 16 (>10)
4*5 = 20 (>10)
4*6 = 24 (>10)
5*1 = 5 (<10)
5*2 = 10 (=10)
5*3 = 15 (>10)
5*4 = 20 (>10)
5*5 = 25 (>10)
5*6 = 30 (>10)
6*1 = 6 (<10)
6*2 = 12 (>10)
6*3 = 18 (>10)
6*4 = 24 (>10)
6*5 = 30 (>10)
6*6 = 36 (>10)
Благоприятных случаев: 1 + 3 + 4 + 4 + 5 = 17
P =
Удачи!