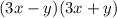

Объяснение:
1/a) 6x-14-5x<=3x-12, x-3x<=14-12, -2x<=2, x>=-1
б) умножаем все на 8, 8x-2(x-3)+x-1 >16, 8x-2x+6+x-1>16,
7x>16-5, 7x>11, x>11/7
2) -2x-3x>-3-12, -5x>-15, x<3 u 7x-4x<=6+12, 3x<=18, x<=6,
ответ : (-Б; 3) Б -бесконечность
3a) x=12 или х=-12, б) 2х+3=7, 2х=4, х=2 или 2х+3= -7, 2х=-10, х=-5
в) 1-3х=37, -3х=36, х=-12 или 1-3х=-37, -3х=-38, х= 38/3=12 2/3
4a) здесь надо решить систему: 4x-1<9 и 4x-1> -9,
4x<10, x<10/4, x<2,5 и 4x>-8, x>-2, ответ: (-2; 2,5)
y'=(x^3)'-(3x^2)'-(72x)'+(5)'=3x^2-6x-72+0=3x^2-6x-72
y'=0
3x^2-6x-72=0
D=b^2-4ac
D=(-6)^2-4×3×(-72)=36+12×72+36+164=36+864=900>0(2различных действительных корня)
Х1, 2=-b+- корень из D/2a
X1=-(-6)+30/2×3=6+30/6=36/6=6
X2=(-6)-30/2×3=6-30/6=-24/6=-4
Получились две точки (6;-4)
Рисуешь числовую прямую и отмечаешь на них данные точки
Для того, чтобы определить экстремумы данных точек, ты должен сначала определить знаки (+) или (-) сверху луча
Сначала берёшь т. (6) и смотришь какое число больше 6,ну например 10,подставляешь 10 в уравнение
3х^2-6х-72=0
И считаешь
3×(10)^2-6×10-72=300-60-72=240-72=168>0
Значит на этом интервале, в области точки 6 будет (+)
След. точка(-4) будет (-)
Ты получил(-) и(+)
Точка(-4)-точка минимума функции
(6)-точка максимума
"(3х-у)" - вторая степень