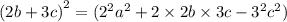
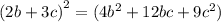
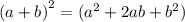
-9; 9
Объяснение:
x²-8|x|-9=0
8|x|=x²-9
|x|=(x²-9)/8
1) x=(x²-9)/8; (x²-9)/8 -(8x)/8=0; x²-8x-9=0; D=64+36=100
x₁=(8-10)/2=-2/2=-1, проверка: (-1)²-8·|-1|-9=1-8-9=-16; -16≠0 - равенство не выполняется ⇒ корень x₁ не подходит.
x₂=(8+10)/2=18/2=9, проверка: 9²-8·|9|-9=9(9-8-1)=9·0=0; 0=0 - равенство выполняется.
2) x=(9-x²)/8; (9-x²)/8 -(8x)/8=0; (9-x²-8x)/8=0 |×(-1)
x²+8x-9=0; D=64+36=100
x₃=(-8-10)/2=-18/2=-9, проверка: (-9)²-8·|-9|-9=9(9-8-1)=9·0=0; 0=0 - равенство выполняется.
x₄=(-8+10)/2=2/2=1, проверка: 1²-8·|1|-9=1-8-9=-16; -16≠0 - равенство не выполняется ⇒ корень x₄ не подходит.
Объяснение:
В знаменателе с точностью до какого-то коэффициента u должен стоять косинус суммы:
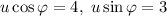
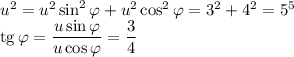
u можно взять положительным, тогда u = 5;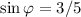 
, 
. Можно было бы взять и отрицательным, при этом были бы другие знаки у синуса и косинуса.
φ тоже можно взять любым, лишь бы у синуса и косинуса были нужные знаки (если u > 0, и то и то будет положительным) и тангенс был равен найденному значению. Я возьму 
, это угол первой четверти.
В числителе должно стоять
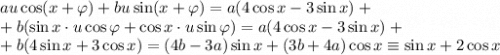
Приравниваем коэффициенты и решаем получившуюся систему:
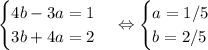
Если
2b это a
3c это b
То тогда