№1
а) √50 > 7
√50 > √7²
√50 > √49
б) 4√6 > 3√7
√4²*6 > √3²*7
√16*6 > √9*7
√96 > √63
№2
а) √(196 * 0,64) = √(14²*(0,8)²) = 14 * 0,8 = 11,2
б) √(72*0,5)=√36=√6² = 6
в) 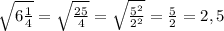
г) √(-2)⁶ = √((-2)³)²=(-2)³= - 8
№3
а) (√3+√2)² = (√3)²+ 2 *√3*√2 + (√2)²= 3 + 2√6 + 2 = 5 +2√6
б) (4 - √5)(4 + √5) = 4² - (√5)² = 16 - 5 = 11
в) 5√12 - 2√27 - 3√3 = 5√(4*3) - 2√(9*3) - 3√3 = 5√(2²*3) - 2√(3²*3) - 3√3 = 5*2√3 - 2*3√3 - 3√3= 10√3 - 6√3 - 3√3 = √3
№4
√(72*а⁵) = √(36*2 * а⁴*а)= √(6²*2 * (а²)² * а) = 6*а²*√(2а)
№5
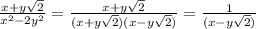
№6
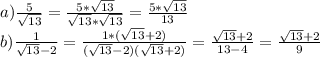
1. АО = ОС по условию,
ВО = OD по условию,
∠АОВ = ∠COD как вертикальные, ⇒
ΔАОВ = ΔCOD по двум сторонам и углу между ними.
2. NK = KP по условию,
∠MNK = ∠EPK по условию,
∠MKN = ∠ЕКР как вертикальные, ⇒
ΔMKN = ΔЕКР по стороне и двум прилежащим к ней углам.
3. АВ = AD по условию,
∠ВАС = ∠DAC по условию,
АС - общая сторона для треугольников ВАС и DAC, ⇒
ΔВАС = ΔDAC по двум сторонам и углу между ними.
4. ВС = AD по условию,
∠CBD = ∠ADB по условию,
BD - общая сторона для треугольников CBD и ADB, ⇒
ΔCBD = ΔADB по двум сторонам и углу между ними.
5. ∠MDF = ∠EDF по условию,
∠MFD = ∠EFD по условию,
DF - общая сторона для треугольников MDF и EDF, ⇒
ΔMDF = ΔEDF по стороне и двум прилежащим к ней углам.
6.
а) ∠МАВ = ∠NBA по условию,
∠МВА = ∠NAB по условию,
АВ - общая сторона для треугольников МАВ и NBA, ⇒
ΔМАВ = ΔNBA по стороне и двум прилежащим к ней углам.
б) АМ = BN из равенства ΔМАВ = ΔNBA (см. п. а))
∠АМН = ∠ВNН из равенства ΔМАВ = ΔNBA,
∠МАН = ∠МАВ - ∠НАВ
∠NBH = ∠NBA - ∠HBA, а так как ∠МАВ = ∠NBA по условию и ∠НВА = ∠НAB по условию, то и
∠MAH = ∠NBH, ⇒
ΔMAH = ΔNBH по стороне и двум прилежащим к ней углам.
7. МК = PN по условию,
MN = PK по условию,
NK - общая сторона для треугольников MNK и PKN, ⇒
ΔMNK = ΔPKN по трем сторонам.
8. ∠ABD = ∠CDB по условию,
∠ADB = ∠CBD по условию,
BD - общая сторона для треугольников ABD и CDB , ⇒
ΔABD = ΔCDB по стороне и двум прилежащим к ней углам.
9. ∠САВ = ∠EFD по условию,
∠АВС = ∠EDF по условию,
АВ = AD + DB
FD = FB + DB, а так как AD = BF по условию, то и
АВ = FD, ⇒
ΔСАВ = ΔEFD по стороне и двум прилежащим к ней углам.
10.
а) АС = ВС по условию,
∠СВЕ = ∠CAD по условию,
угол при вершине С - общий для треугольников СВЕ и CAD, ⇒
ΔСВЕ = ΔCAD по стороне и двум прилежащим к ней углам.
б) ∠ADC = ∠BEC из равенства треугольников СВЕ и CAD, ⇒
∠BDF = ∠AEF как смежные с равными углами,
∠DBF = ∠EAF по условию,
BD = BC - DC
AE = AC - EC, а так как ВС = АС по условию, и DC = EC из равенства треугольников СВЕ и CAD, то и BD = AE, ⇒
ΔBDF = ΔAEF по стороне и двум прилежащим к ней углам.
11. КН = ЕН по условию,
FK = PE по условию,
∠FKH = ∠PEH как смежные с равными углами, ⇒
ΔFKH = ΔPEH по двум сторонам и углу между ними.
12. DE = CE по условию,
∠ADE = ∠BCE как смежные с равными углами,
∠AED = ∠BEC как вертикальные, ⇒
ΔAED = ΔBEC по стороне и двум прилежащим к ней углам.
Объяснение:
792
Объяснение: