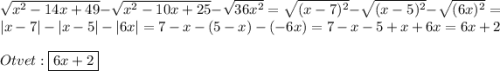
х ( км/ч ) - скорость первого поезда.
y ( км/ч ) - скорость второго поезда.
10х ( км ) - расстояние, которое проедет первый поезд за 10 ч.
10y ( км ) - расстояние, которое проедет второй поезд за 10 ч.
10х+10y ( км ) - расстояние между городами, которое по условию задачи равно 650 км.
Получаем первое уравнение: 10х+10у=650
8 ч + 4 ч 20 мин = 12 ч 20 мин
12 ч 20 мин =12 20\60ч=740\60ч
740\60х(км) расстояние которое проедет первый поезд за 12 ч 20 мин
8y ( км ) - расстояние, которое проедет второй поезд за 8 ч.
740\60 х + 8y ( км ) - расстояние между городами, которое по условию задачи равно 650 км.
Получаем второе уравнение: 740\60х+8у=650
получаем систему:(см.влож)
ответ: первый поезд проходит 30 км/ч, второй 35 км/ч.

ответ: x1=1 ; x2= (-1+√33)/2 ; x3= (-1-√33)/2
Объяснение:
Необходимо решить следующее уравнение:
x^3+8=9*∛(9x-8)
Преобразуем данное уравнение:
x^3= 9*∛(9x-8) -8
x=∛( 9*∛(9x-8) -8 )
Пусть: f(x)=∛(9x-8)
Тогда уравнение принимает вид:
x=f (f(x) )
Рассмотри вс уравнение вида:
x=f(x)
Предположим , что оно имеет корень x0 , то есть верно равенство:
1) x0=f(x0)
Вернемся к уравнению:
2) f( f(x) )=x
Можно заметить , что x=x0 так же является корнем этого уравнения.
Действительно , если подставить x0 имеем:
f ( f(x0) )=x0
Поскольку : f(x0)=x0 , то f ( f(x0) )=f(x0)
Откуда уравнение эквивалентно следующему:
f(x0)=x0 , что эквивалентно уравнению 1 , а значит x0 является корнем уравнения : f( f(x) )=x.
То есть все те корни ,что имеет уравнение: f(x)=x , обязательно имеет и уравнение : f( f(x) )=x
Запишем уравнение f(x)=x для нашей функции:
∛(9x-8)=x
x^3-9x+8=0
(x^3-1) -9*(x-1)=0
(x-1)*(x^2+x+1) -9*(x-1)=0
(x-1)*(x^2+x-8)=0
x1=1
x^2+x-8=0
D=1+32=22
x23=(-1+-√33)/2
Покажем теперь что уравнение :
x=∛( 9*∛(9x-8) -8 )
не имеет других корней кроме выше приведенных. ( то есть данные уравнения имеют идентичные корни)
Не трудно заметить ,что функция : f(x)=∛(9x-8) монотонно возрастает.
То есть ,для такой функции справедливо следующее утверждение:
Если x1>x2 , то f(x1)>f(x2)
Предположим, что x0 корень уравнения :
f( f(x) )=x , то есть верно что:
f( f(x0) )=x0
Предположим , что x0 не является корнем уравнения f(x)=x , то
есть f(x0)≠x0
Пусть: f(x0)>x0
Тогда согласно утверждению выше:
f( f(x0) )>f(x0)
Но поскольку f (f (x0) )=x0 , то
x0>f(x0) , что противоречит неравенству: f(x0)>x0.
То есть такое невозможно.
Аналогично доказывается невозможность случая: f(x0)<x0
f( f(x0) )<f(x0)
x0<f(x0) , то есть противоречие.
Вывод: если уравнение f(f(x))=0 имеет корень x0, то этот корень имеет и уравнение f(x)=x , но так же мы до этого показали то что , если f(x)=x имеет корень x0, то и уравнение f(f(x))=0 имеет этот корень.
Таким образом заключаем , что уравнение:
x=∛( 9*∛(9x-8) -8 )
имеет то же самое множество корней , что и уравнение:
x= ∛(9x-8)
ответ: x1=1 ; x2= (-1+√33)/2 ; x3= (-1-√33)/2