Объяснение:
Действуем по такому методу:
Если знаменатель дроби — квадратный корень, чтобы избавиться от иррациональности в знаменателе умножаем и числитель, и знаменатель на сопряженный на квадратный корень, находящийся в знаменателе (это, конечно, не всегда, точнее сказать, надо умножить на такое число, чтобы при перемножении знаменателя с ним убирался корень)
1) 
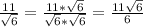
2) 
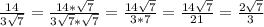
3)
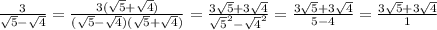вот здесь, как раз-то число, на которое умножаем, это не совсем знаменатель, но именно при перемножении с ним, мы можем избавиться от иррациональности.
P.S. если решил правильно, отметь как лучший)
В решении.
Объяснение:
Найдите целые решения неравенства:
-х²+10х-21>0
Приравнять к нулю и решить квадратное уравнение:
-х² + 10х - 21 = 0/-1
х² - 10х + 21 = 0
D=b²-4ac =100 - 84 = 16 √D=4
х₁=(-b-√D)/2a
х₁=(10-4)/2
х₁=6/2
х₁=3;
х₂=(-b+√D)/2a
х₂=(10+4)/2
х₂=14/2
х₂=7.
Уравнение квадратичной функции, график - парабола, ветви направлены вниз, пересекают ось Ох в точках х= 3 и х= 7.
Решение неравенства: х∈(3; 7).
Неравенство строгое, значения х= 3 и х= 7 не входят в решение, поэтому целые решения неравенства: 4; 5; 6.
Приводим к общему знаменателю:
(6a-3(a+b))/a^2-b^2 = (3a-3b)/a^2-b^2 = 3(a-b)/a^2-b^2 = 3 / (a + b) ..
Дальше, что с этим делать, не особо понятно, условий не хватает