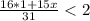
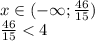то есть да может , так как 
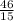ее целая часть равна 3 , а она натуральное число , и найдется набор таких чисел что среднее арифметическое будет меньше 2 , так как в условий не сказано что , сам набор может состоят так только из разных натуральных чисел. 
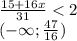, целая часть этого числа равна 
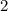, то есть не может , так как в сумме 
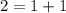, и по количеству в этом наборе минимальное есть 16 единиц . 
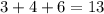так как мы ранее доказали что , есть не менее 16 единиц , и того 
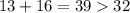что удовлетворяет условию .
Объяснение:
Сумма 1+3+...+(2n-1) значит сумму всех нечетных натуральных чисел начиная с 1 и заканчивая 2n-1
Так как при n=1 =>2n-1=2*1-1=1, то для базы индукции сумма начинается с 1 и ею же заканчивается, т.е. состоит только из одного числа 1,
а уже при n=2 (1+3), n=3 (1+3+5) и т.д., и больше будет два и больше слагаемых, и последний член предстанет "более явно",
при n=1 : 1+3+...+(2n-1) =1=(2n-1)
формула 2n-1 показывает какой вид имеет n-ое слагаемое суммы, но в случае n=1 сумма состоит из одного единственного слагаемого 1
12ab + 16a - 3b - 4 = (12ab + 16a) - (3b + 4) = 4a(3b + 4) - (3b + 4) =
= (3b + 4)(4a - 1)
Если a = 0,35 , а b = - 1 , то
(3 * (- 1) + 4)(4 * 0,35 - 1) = (- 3 + 4)(1,4 - 1) = 1 * 0,4 = 0,4