Ну тут всё очень просто.
Пусть х см - длина стороны BC, тогда AB (x+3) см,а площадь прямоугольника равна 28 см². Т.к. это прямоугольник, то AB=CD, BC=AD (по свойству).
Составим и решим уравнение.
S=ab (то есть произведения двух его смежных сторон)
Для нашего случая : S=x(x+3)
x(x+3)=28
x²+3x-28=0
По теореме Виета корни здесь будут -7 и 4.
-7 мы сразу можем не принимать, т.к. длина стороны это всегда положительное число.
Если x=4, то стороны BC и AD равны по 4 см.
4+3=7 см - стороны AB и BC.
ответ. 4 см и 7 см.
1. Будем доказывать методом математической индукции.
Проверяем истинность утверждения при n = 1:
а) 2*49 + 16 + 40 = 154 = 11*14 - делится на 11.
б) Предположим, что 2*7^(2k) + 16^k +8*5^k - делится на 11. Где k - произвольное натуральное число.
в) Докажем, что тогда при n = k+1 полученное выражение - тоже делится на 11:
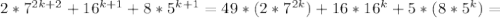
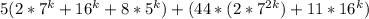
Теперь четко видно что оба больших слагаемых делятся на 11:
первое - исходя из предположения, второе - имеет 11 как общий сомножитель для своих слагаемых.
Итак мы доказали , что если при произвольном n= k выражение делится на 11, то и при n = k+1 выражение делится на 11.
Значит исходное выражение делится на 11. что и требовалось доказать.
2)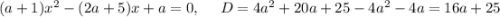
D>0 a>-25/16 a>-1,5625
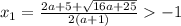
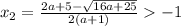
Разбиваем ОДЗ на две части:
а) (-1; беск)
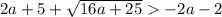
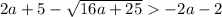
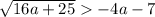
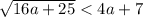
Первое из написанных неравенств верно. Проверим второе:
16a+25<16a^2+56a+49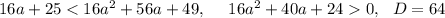
Корни -1; -1,5 Решение с учетом ОДЗ: (-1; беск)
б) (-1,5625; -1)
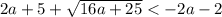
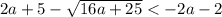
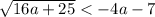
Правая чать на выбранной области - отрицательна, что недопустимо. Здесь решений нет.
ответ: (-1; бескон).
3.
![[\sqrt{1-sin^2153}+\sqrt{tg^2207-sin^2207}]sin63=[-cos153+\frac{sin^2207}{-cos207}]sin63](/tpl/images/0025/6265/72073.png)
![=[sin63+\frac{cos^263}{sin63}]sin63=sin^263+cos^263=1](/tpl/images/0025/6265/378ae.png)
ответ: 1