 — общее число человек на экзамене по математике.
— общее число человек на экзамене по математике. ,
,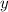 . Итак, число верно решивших относится к числу не решивших вовсе, как 5:3. Получается:
. Итак, число верно решивших относится к числу не решивших вовсе, как 5:3. Получается: 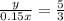 , отсюда
, отсюда 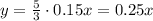 .
. , решили с ошибками 144, решили правильно
, решили с ошибками 144, решили правильно 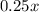 . Вместе эти три группы есть общее число человек на экзамене, то есть
. Вместе эти три группы есть общее число человек на экзамене, то есть  . Получаем:
. Получаем: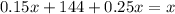
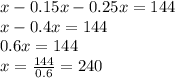
√7*4-3=√28-3=√25=5
√36*0,81=√36*√0,81=6*0,9=5,4