(см. объяснение)
Объяснение:
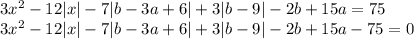
Введем функцию  .
.
Заметим, что перед нами уравнение двух парабол, склеивающихся в фиксированной точке 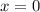 .
.
Этот график может ездить только вверх-вниз в зависимости от значений параметров  и
и 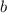 .
.
Уравнение  может иметь ровно два корня при любом значении параметра
может иметь ровно два корня при любом значении параметра 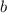 только, если
только, если 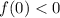 .
.
Тогда перейдем к неравенству:
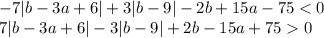
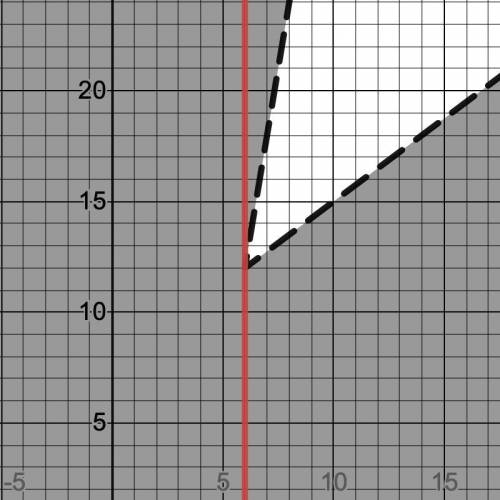
Построим его в координатах 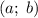 .
.
(см. прикрепленный файл)
Получили, что при 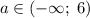 исходное уравнение имеет ровно два различных корня при любом значении параметра
исходное уравнение имеет ровно два различных корня при любом значении параметра 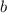 .
.
ответим теперь на вопрос задачи: ниже 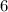 .
.
Задание выполнено!
Решение.
Поскольку 3000 и 1980 делятся на 60, Володя сможет снять лишь сумму, кратную 60 рублям. Максимальное число, кратное 60 и не превосходящее 5000, - это 4980.
Докажем, что снять 4980 рублей возможно. Произведем следующие операции: 5000-3000=2000, 2000+1980=3980, 3980-3000=980, 980+1980=2960, 2960+1980=4940. Сумма, лежащая на счете, уменьшилась на 60 рублей.
Проделав аналогичную процедуру 16 раз, Петя снимет 960 рублей. Затем он может снять 3000, положить 1980 и снова снять 3000. В результате у него будет 4980 рублей.
=(у-7)(5-х)
б) 5a^2+10ay+5y^2=5(a^2+2ay+y^2)=5(а+у)^2=
=5(а+у)(а+у)