Объяснение:
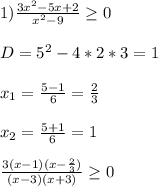
+ - + - +
_____-3_________2/3______1___________3_______
x∈(-∞;3)∪[2/3; 1]∪(3; +∞)
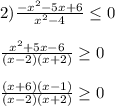
+ - + - +
_______-6____________-2______1______2______
x∈(-∞; -6]∪(-2; 1]∪(2; +∞)
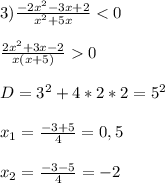
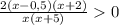
+ - + - +
_____-5__________-2_____0____0,5______
x∈(-∞; -5)∪(-2; 0)∪(0,5; +∞)
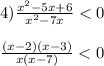
+ - + - +
_______0_______2______3_________7________
x∈(0;2)∪(3;7)
1) Оценим разность
( х + 2)² - 8х = х² + 4х + 4 - 8х = х² - 4х + 4 = ( х - 2 )²
( х + 2)²
2) Оценим разность:
х² + 2х + 2 - 0 = (х² + 2х + 1) + 1 = ( х + 1)² + 1 > 0 при всех значениях х, т.к. по определению квадрата ( х + 1)²