Объяснение:
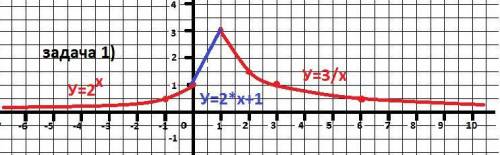
Задача 1) - рисунок к задаче в приложении.
При х=0 обе первых части графика совпадают в точке (0;1)
А третья функция: у = 3/х при х=1 равна
у(3) = 3/3 = 1.
Задача сводится провести прямую через две точки А(0;1) и В(1;3)
ДАНО: А(0;1), В(1;3)
НАЙТИ: Y = k*x + b
РЕШЕНИЕ
1) k = ΔY/ΔX = (Аy-Вy)/(Аx-Вx)=(1-(3))/(0-(1))=2 - коэффициент наклона прямой
2) b=Аy-k*Аx=1-(2)*0= 1- сдвиг по оси ОУ
Уравнение Y(АВ) = 2*x+1 - функция на втором участке.
ОТВЕТ: а = 2 - коэффициент.
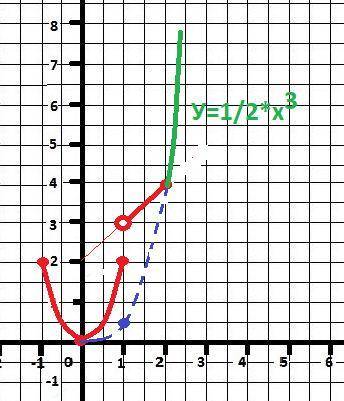
Задача 2) - рисунок в приложении.
При х = 2 на втором участке у = х + 2 = 4.
Задача сводится найти решение
y(2) = a*x³ = a*2³ = a*8 = 4
a = 4/8 = 0.5 = а - коэффициент - ответ.
Даны точки A(-1;4), B(3;1), C(3,4). Найдите вектор c= 2 CA+3ABОбозначим точку пересечения плоскости β отрезком CD буквой О.
DD1║CC1, CD- секущая, ⇒ накрестлежащие ∠D=∠C, вертикальные углы при О равны, ⇒ ∆ DOD1 подобен ∆ COC1 по первому признаку.
k=CC1:DD1=6/√3:√3=2
Тогда СО=2DO=²/₃ СD
ЕО=СО-СЕ
EO= \frac{2}{3} CD- \frac{1}{2} CD= \frac{1}{6} CDEO=
3
2
CD−
2
1
CD=
6
1
CD
∆ COC1 подобен ∆ EOE1 по первому признаку подобия ( ∠С=∠Е - соответственные при пересечении параллельных прямых ЕЕ1 и СС1 секущей CD, угол О - общий).
k= \frac{CO}{EO} = \frac{ \frac{2}{3} CD}{ \frac{1}{6} CD}= \frac{2*6}{3}= 4k=
EO
CO
=
6
1
CD
3
2
CD
=
3
2∗6
=4 ⇒
E E_{1}= \frac{6}{ \sqrt{3}}:4= \frac{6* \sqrt{3} }{ \sqrt{3}* \sqrt{3} *4}= \frac{ \sqrt{3}}{2} smEE
1
=
3
6
:4=
3
∗
3
∗4
6∗
3
=
2
3
sm