Решить : имеется много одинаковых кубиков. из них склеили всевозможные фигуры , состоящие из 5 кубиков, соединённых гранями так, что совпали вершины склеиваемых граней. а затем подсчитали площади поверхностей полученных фигур , состоящих из равных квадратов. сколько различных значений получили?

👇

Увидеть ответ

Ответ:

liza1383

27.11.2020

У пяти кубиков всего 5 * 6 = 30 граней.

Каждое соединение двух кубиков уменьшает их количество на 2 грани.

Всего из пяти кубиков можно построить 15 фигур - на рисунке в приложении.

У большинства из них - четыре общих грани и 30 - 8 = 22 открытых грани.

Только у рис. 5 и 15 - по 5 общих грани и 20 граней открыты.

ответ: Два варианта числа открытых граней.

Решить : имеется много одинаковых кубиков. из них склеили всевозможные фигуры , состоящие из 5 кубик

4,7(34 оценок)

Открыть все ответы

Ответ:

indirsuleimano

27.11.2020

ОКАНЧИВАЕТСЯ НА 4.

1)ЧИСЛО 2 В СТЕПЕНИ 99 ОКАНЧИВАЕТСЯ НА ЦИФРУ 8.

если составить небольшую табличку,

2 в степени 1 оканчивается на 2

2 2 4

2 3 8

2 4 6

если продолжать дальше,то последовательность чисел будет постоянно повторяться,то есть любая степень числа 2 может оканчиваться на 2,4,8 или на 6 (ну,еще есть 2 в степени ноль,но это только единичный случай)

с этой таблички вычисляем,что 2 в степени 99 оканчивается на цифру 8.

2) теперь смотрим таблицу умножения на 7.

число,оканчивающееся на цифру 8 - только 28 (4*7=28),соответственно,при делении на 7 числа,оканчивающегося на цифру 8 может получиться только число,оканчивающееся на цифру 4.

4,7(81 оценок)

Ответ:

Амаз123

27.11.2020

Есть правило нахождении предела отношения дробно-рациональной функции при х---> к бескон.Если многочлен в числителе имеет степень, равную степени многочлена в знаменателе, то предел равен отношению коэффициентов перед СТАРШИМИ степенями.Доказывается это с деления числителя и знаменателя на старшую степень и учёта того, что константа, делённая на бесконечно большую велмчину равна 0 (беск.малой величине).
В 1 примере старшая степень числителя первая и коэффициент перед ней равен 1.В знаменателе старш.степень первая и старший коэффю=1.Поэтому предел равен 1:1=1. Если решать пример с деления на старш.степень, то получим:

$lim_{x\to \infty }\frac{x+1}{x-2}=lim_{x\to \infty }\frac{\frac{x}{x}+\frac{1}{x}}{\frac{x}{x}-\frac{2}{x}}=lim\frac{1+\frac{1}{x}}{1-\frac{2}{x}}=[\frac{1+0}{1-0}]=\frac{1}{1}=1$

Конечно, удобнее пользоваться готовым правилом.

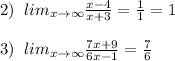
$2)\; \; lim_{x\to \infty}\frac{x-4}{x+3}=\frac{1}{1}=1\\\\3)\; \; lim_{x\to \infty}\frac{7x+9}{6x-1}=\frac{7}{6}$

Если степень многочлена в числителе меньше степени многочлена в знаменателе, то предел будет равен 0.
Если степень многочлена в числ. больше степени мног. в знаменателе, то предел равен бесконечности.
Например:

$lim_{x\to \infty }\frac{x+3}{5x^2+2x-5}=0,tak\; \; kak\\\\lim_{x\to \infty }\frac{\frac{x}{x^2}+\frac{3}{x^2}}{\frac{5x^2}{x^2}+\frac{2x}{x^2}-\frac{5}{x^2}}=lim\frac{\frac{1}{x}+\frac{3}{x^2}}{5+\frac{2}{x}-\frac{5}{x^2}}=[\frac{0+0}{5+0-0}]=\frac{0}{5}=0$