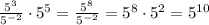
1
Объяснение:
Угол наклона прямой в координатной плоскости изменяется в промежутке [0; π) за исключением π/2, то есть по значению тангенса можно однозначно определить угол. Вспомним, что прямые параллельны, если соответственные углы равны. Если принять за секущую ось Ox, то можно сравнить углы наклона. А для этого уже достаточно сравнить их тангенсы!
Тангенс угла наклона касательной можно найти с производной — это значение производной в данной точке. Тангенс угла наклона прямой — это коэффициент перед x. Тогда:
— если подставить вместо x какое-то значение, получим тангенс угла наклона касательной. Тангенс угла наклона прямой — это 1 (y = 1*x + 8). Поэтому, чтобы прямые были параллельны, нужно приравнять производную и тангенс угла наклона прямой:
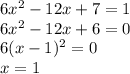
нужно построить в одной системе координат графики функций у = х2 и
у = 2х + 3 . Они пересекаются в двух точках А(- 1; 1) и В(3; 9). Корнями уравнения служат абсциссы точек А и В, значит, х1 = -1, х2 = 3.
х²=2х+3 х²-2х-3 Построим график функции у = х2 - 2х - 3
1) Имеем а = 1, b = -2, х=-b/2a=1, у = f(1) = I2 - 2 - 3 = - 4. Значит, вершиной параболы служит точка (1;- 4), а осью параболы — прямая х = 1.
2) Возьмем на оси х две точки, симметричные относительно оси параболы: точки х = -1 и х =3. Имеем /(-1) = /(3) = 0; отметим в координатной плоскости точки (-1; 0) и (3; 0).
3) Через точки (-1; 0), (1; -4), (3; 0) проводим параболу (рис.1).Корнями уравнения
х2 - 2х - 3 = 0 являются абсциссы точек пересечения параболы с осью х; находим
x1= -1,
x2 = 3
рисовать не буду нет времени
его можно решить
Объяснение:
