Немного теории. Систему уравнений можно записать в следующем виде:
A·x = b
где A - матрица коэффициентов, x - вектор-столбец переменных, b - вектор-столбец свободных членов.
Умножим эту систему на обратную матрицу коэффициентов A⁻¹ слева. Тогда:
A⁻¹·A·x = A⁻¹·b
x = A⁻¹·b
Таким образом, чтобы решить систему уравнений, нужно найти обратную матрицу коэффициентов и умножить ее на вектор-столбец свободных членов.
1) Обратная матрица
Будем искать обратную матрицу через алгебраические дополнения. Для начала найдем определитель матрицы A :
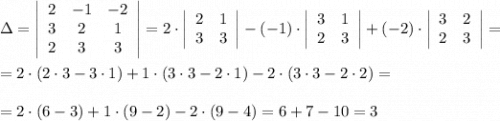
Найдем элементы матрицы алгебраических дополнений:
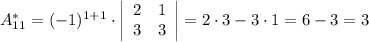
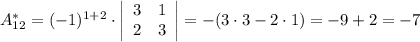
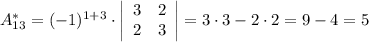

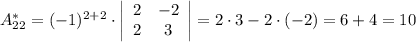
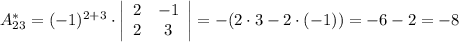
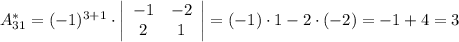
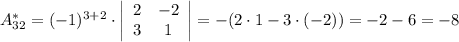
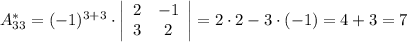
Тогда:

Транспонированная матрица алгебраических дополнений:
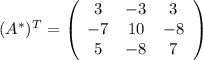
Обратная матрица:
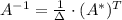
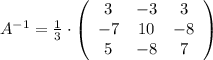
2) Вектор-столбец переменных
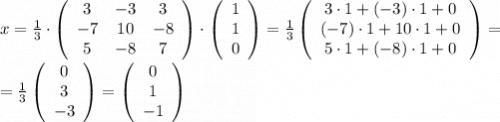
x₁ = 0;
x₂ = 1;
x₃ = -1.
Даны точки A(-1;4), B(3;1), C(3,4). Найдите вектор c= 2 CA+3ABОбозначим точку пересечения плоскости β отрезком CD буквой О.
DD1║CC1, CD- секущая, ⇒ накрестлежащие ∠D=∠C, вертикальные углы при О равны, ⇒ ∆ DOD1 подобен ∆ COC1 по первому признаку.
k=CC1:DD1=6/√3:√3=2
Тогда СО=2DO=²/₃ СD
ЕО=СО-СЕ
EO= \frac{2}{3} CD- \frac{1}{2} CD= \frac{1}{6} CDEO=
3
2
CD−
2
1
CD=
6
1
CD
∆ COC1 подобен ∆ EOE1 по первому признаку подобия ( ∠С=∠Е - соответственные при пересечении параллельных прямых ЕЕ1 и СС1 секущей CD, угол О - общий).
k= \frac{CO}{EO} = \frac{ \frac{2}{3} CD}{ \frac{1}{6} CD}= \frac{2*6}{3}= 4k=
EO
CO
=
6
1
CD
3
2
CD
=
3
2∗6
=4 ⇒
E E_{1}= \frac{6}{ \sqrt{3}}:4= \frac{6* \sqrt{3} }{ \sqrt{3}* \sqrt{3} *4}= \frac{ \sqrt{3}}{2} smEE
1
=
3
6
:4=
3
∗
3
∗4
6∗
3
=
2
3
sm