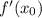производная функции в данной точке. А 
точка касания по иксу.
мы должны найти производную общего типа этой функции.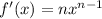
- где n это степень.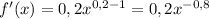
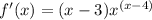
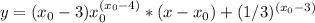
и получаешь уравнение касательной.
1. 3(y-1)² +6y=3(y²-2y+1)+6y=3y²-6y+3+6y=3y²+3, можно вынести 3 за скобку 3(y²+1)
2. 3(x+y)² - 6xy= 3(x²+2xy+y²)-6xy=3x²+6xy+3y²-6xy=3x²+3y²
3. (x-y)²-x(x-2y)=x²-2xy+y²-x²+2xy=y²
4. (x-2)(x+4) - 2x(1+x)=x(x+4)-2(x+4)-2x-2x²=x²+4x-2x-8-2x-2x²= -x²-8
5. 3a(2a-1) - 2a(4+3a)=6a²-3a-8a-6a²= -11a
6. (a-c)(a+c)-c(3a-c)=a²-c²-3ac+c²=a²-3ac
7. (m+3)²-(m-2)(m+2)=m²+6m+9-(m²-4)=m²+6m+9-m²+4=6m+13
8. (a-2)(a-4)-(a+1)²=a(a+4)-2(a+4)-(a²+2a+1)=a²+4a-2a-8-a²-2a-1= -9
9. (b-4)(b+2)-(b-1)²=b(b+2)-4(b+2)-(b²-2b+1)=b²+2b-4b-8-b²+2b-1= -9
Если что не понятно - спрашивайте.