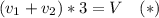
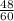 часа. То есть, разделив на 12 и числитель и знаменатель, получим
часа. То есть, разделив на 12 и числитель и знаменатель, получим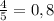 часа.
часа.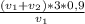 часов работал только первый насос.
часов работал только первый насос.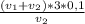 часа - время работы второго насоса.
часа - время работы второго насоса.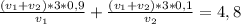
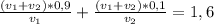
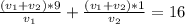
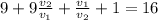 Перенесем свободные члены в правую часть
Перенесем свободные члены в правую часть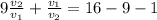
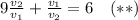
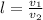
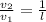
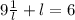

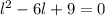
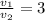
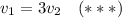
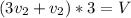
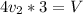
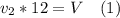
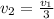 то, подставив в (1), получаем
то, подставив в (1), получаем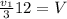
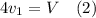
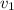 , наполнит бак объёмом V за 4 часа.
, наполнит бак объёмом V за 4 часа. 
Найдем ОДЗ:
x<0
x<0
l 2x01 l -x =0
x<0
l 2x-1 l -x=0
x<0
x=1
x=1/3
x∈(-∞;0)∪{1/3;1}
Окончательное ОДЗ:
x∈[9;1/3)∪(1/3;1)∪(1;+∞);
Теперь дело за малым(
Посмотрим на ВСЕ случаи :
При открытии модуля опять 2 случая, если нужно розпишу, а так:
Находим пересечения из первой системы : x∈(-∞;1/4)
Из второй системы: x∈(1/3;1)
Находим их объединение :
Не забываем про ОДЗ и находим их общее объединение, что и будет ответом:
ответ: