Номер 463.
1) -7. Взять -7 мы можем, т.к. по условию оно нам подходит.
2) -4. Взять -3,7 не можем, т.к. нам по условию надо выбрать целое число.
3) 4. Взять 4,8 не можем, т.к. нам по условию надо выбрать целое число.
4) -6. Взять -5,6 не можем, т.к. нам по условию надо выбрать целое число.
Номере 464.
1) -11. Взять -11,9 не можем, т.к. нам по условию надо выбрать целое число.
2) -5. Взять -5,2 не можем, т.к. нам по условию надо выбрать целое число.
3) 9. Взять 8,1 не можем, т.к. нам по условию надо выбрать целое число.
4) -8. Взять -8,1 не можем, т.к. нам по условию надо выбрать целое число.
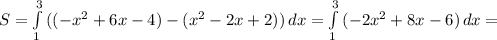
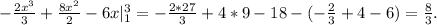
б) (a-7b)²= формула квадрата разницы = а²-14ав+49в²;
в) (x-y)(x+y)= формула разницы квадратов =х²-у²;
г) (2x-0,7y²)(0,7y²+2x)=(2x-0,7y²)(2x+0,7y²)= формула разницы квадратов= 4х²-0,49у^4.