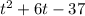
Найдем сначала уравнение секущей:
Она проходит через две точки:х1=-1, у1 = 2*(-1)^2 = 2
и х2 = 2, у2 = 2*2^2 = 8
Ищем уравнение секущей в виде: y=kx+b
Подставим сюда две наши точки и решим систему, найдем k:
-k+b=2
2k+b=8 Вычтем из второго первое: 3k = 6, k= 2.
Наша искомая касательная должна быть параллельна секущей, значит имее такой же угловой коэффициент. k=2
Найдем точку касания, приравняв производную нашей ф-ии двум:
Y' = 4x = 2
x = 1/2
Уравнение касательной к ф-ии в т.х0:
у = у(х0) + y'(x0)(x-x0)
Унас х0 = 1/2, у(1/2) = 2*(1/4) = 1/2, y'(1/2)= 2.
Тогда получим:
у = 1/2 + 2(х - 1/2)
у = 2х -0,5 - искомое уравнение касательной.
Решение. В данном случае объем выборки n = 15. Упорядочим элементы выборки по величине, получим вариационный ряд 2, 2, 3, 4, 4, 5, 5, 5, 7, 7, 7, 7, 10, 10. Найдем размах выборки ω=10-2= 8. Различными в заданной выборке являются элементы z1 = 2, z2 =3, z3 = 4 , z4 = 5 , z5 = 7 , z6 = 10 ; их частоты соответственно равны n1 = 3, n2=1, n3 = 2, n4 = 3 , n5 = 4, n6 = 2. Статистический ряд исходной выборки можно записать в виде следующей таблицы:
zi
ni
Для контроля правильности записи находим . При большом объеме выборки ее элементы рекомендуется объединять в группы (разряды), представляя результаты опытов в виде группированного статистического ряда. В этом случае интервал, содержащий все элементы выборки, разбивается на k непересекающихся интервалов. Вычисления упрощаются, если эти интервалы имеют одинаковую длину . В дальнейшем рассматривается именно этот случай. После того как частичные интервалы выбраны, определяют частоты - количество ni элементов выборки, попавших в i-й интервал (элемент, совпадающий с верхней границей интервала, относится к следующему интервалу). Получающийся статистический ряд в верхней строке содержит середины zi интервалов группировки, а в нижней — частоты ni (i = 1
Объяснение:
Наверное так( не моя работа, взял с другого ответа)